题目内容
1.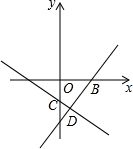 已知:如图,一次函数y=$\frac{4}{3}$x+n与x轴交于点B,一次函数y=-$\frac{2}{3}$x+m与y轴交于点C,且它们的图象都经过点D(1,-$\frac{8}{3}$).
已知:如图,一次函数y=$\frac{4}{3}$x+n与x轴交于点B,一次函数y=-$\frac{2}{3}$x+m与y轴交于点C,且它们的图象都经过点D(1,-$\frac{8}{3}$).(1)求B、C两点的坐标;
(2)设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值;
(3)在(2)的条件下,在第四象限内,以CP为腰作等腰Rt△CPQ,求点Q的坐标.
分析 (1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得B、C点坐标;
(2)根据面积的和差,可得关于t的方程,根据解方程,可得答案;
(3)根据全等三角形的判定与性质,可得PF,PQ的长,根据点的坐标的意义,可得Q点的坐标.
解答 解:(1)将(1,-$\frac{8}{3}$)代入y=$\frac{4}{3}$x+n,解得n=-4,
即y=$\frac{4}{3}$x-4,当y=0时,$\frac{4}{3}$x-4=0.
解得x=3,
即B点坐标为(3,0);
将(1,-$\frac{8}{3}$)代入y=-$\frac{2}{3}$x+m,解得n=-2,
即y=-$\frac{2}{3}$x-2,当x=0时,y=-$\frac{2}{3}$x-2=-2.
即C点坐标为(0,-2);
(2)连接PC,PD,
如图1 ,
,
S△BDP=$\frac{1}{2}$(t-3)×|-$\frac{8}{3}$|=$\frac{4}{3}$(t-3);
当y=0时,-$\frac{2}{3}$x-2=0,解得x=-3,即E点坐标为(-3,0).
S△CDP=S△DPE-S△CPE=$\frac{1}{2}$(t+3)×$\frac{8}{3}$-$\frac{1}{2}$×(t+3)×|-2|=$\frac{1}{3}$(t+3).
由△BDP和△CDP的面积相等,得
$\frac{1}{3}$(t+3)=$\frac{4}{3}$(t-3).
解得t=5,
(3)如图2 ,
,
QF⊥x轴于F点.
由△CPQ是等腰直角三角形,得
CP=PQ,∠CPQ=90°.
∠OPC+∠PCO=90°,∠OPC+∠QPF=90°,
∴∠PCO=∠QPF.
在△CPO和△PQF中,$\left\{\begin{array}{l}{∠O=∠PFQ}\\{∠PCO=∠QPF}\\{CP=PQ}\end{array}\right.$,
∴△CPO≌△PQF(AAS),
∴PF=OC=2,FQ=OP=5,
Q点的横坐标为5+2=7,Q点的纵坐标为-5,
即Q(7,-5).
点评 本题考查了一次函数综合题,利用待定系数法求函数解析式;利用面积的和差得出关于t的方程是解题关键;利用全等三角形的判定与性质得出PF=OC=2,FQ=OP=5是解题关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
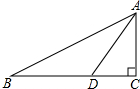 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
| A. | 1.5(1+x)=4.5 | B. | 1.5(1+2x)=4.5 | ||
| C. | 1.5(1+x)2=4.5 | D. | 1.5(1+x)+1.4(1+x)2=4.5 |