题目内容
16.若点A(-4,0)、B(2,0)(1)在y轴上找一点C,使之满足S△ABC=8.求点C的坐标;
(2)在坐标平面内找一点C,能满足S△ABC=8的点C有多少个?这些点的位置有何特点?
分析 (1)设点C(0,a),根据三角形面积公式列出方程即可解决.
(2)根据同底等高三角形面积相等即可解决.
解答 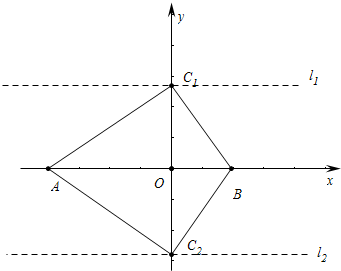 解:(1)如图,设点C(0,a),
解:(1)如图,设点C(0,a),
∵S△ABC=8,
∴$\frac{1}{2}$×6×|a|=8,
∴a=$±\frac{8}{3}$,
∴点C坐标为(0,$\frac{8}{3}$)或(0,-$\frac{8}{3}$).
(2)在坐标平面内找一点C,能满足S△ABC=8的点C有无数个,
这些点在平行于x轴到x轴的距离等于$\frac{8}{3}$的这些l1和直线l2上,如图所示.
点评 本题考查坐标与图形的性质、三角形的面积有关的问题,理解同底等高三角形面积相等,是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
6.某小组7位同学的中考体育测试成绩(满分50分)依次为47,50,49,47,50,48,50,则这组数据的众数与中位数分别是( )
| A. | 50,47 | B. | 50,49 | C. | 49,50 | D. | 50,48 |
8.某童装专卖店,为了吸引顾客,在“六一”儿童节当天举办了甲、乙两种品牌童装有奖酬宾活动,凡购物满100元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同.摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如表).
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的童装?并说明理由.
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的童装?并说明理由.
| 甲种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 15 | 30 | 15 | |
| 乙种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 30 | 15 | 30 |
5.已知点P(2,6)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,则k的值是( )
| A. | 3 | B. | 12 | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
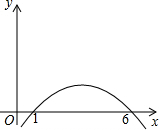 变量x与y之间的函数关系如图所示,请回答下列问题:
变量x与y之间的函数关系如图所示,请回答下列问题: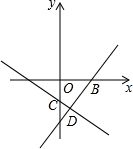 已知:如图,一次函数y=$\frac{4}{3}$x+n与x轴交于点B,一次函数y=-$\frac{2}{3}$x+m与y轴交于点C,且它们的图象都经过点D(1,-$\frac{8}{3}$).
已知:如图,一次函数y=$\frac{4}{3}$x+n与x轴交于点B,一次函数y=-$\frac{2}{3}$x+m与y轴交于点C,且它们的图象都经过点D(1,-$\frac{8}{3}$).