题目内容
14.有一水池能装水1000升,现水池中有水500升,有一进水管每小时进水20升,水池中的水量y(升)随进水时间x(小时)的变化而变化.(1)写出y与x的函数关系式;
(2)求进水10小时,水池中的水量.
分析 (1)根据放满水的时间可找出时间x的取值范围,结合题意即可得出y与x的函数关系式;
(2)将t=10代入(1)的解析式中,即可求出此时水池中的水量.
解答 解:(1)水池装满水的时间=(1000-500)÷20=500÷20=25小时.
故0≤x≤25.
根据题意可知:y=20x+500.
故y与x的函数关系式为y=20x+500(0≤x≤25).
(2)令t=10,则有y=20×10+500=200+500=700升.
故进水10小时,水池中的水量为700升.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据放满水的时间找出x的取值范围,结合题意找出y与x的函数关系式;(2)将x=10代入(1)的解析式即可.

练习册系列答案
相关题目
5.若m>n,则下列式子中错误的是( )
| A. | m-2>n-2 | B. | $\frac{m}{2}>\frac{n}{2}$ | C. | -2m>-2n | D. | m+2>n+2 |
9.2015的相反数是( )
| A. | $\frac{1}{2015}$ | B. | -2015 | C. | 2015 | D. | -$\frac{1}{2015}$ |
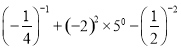
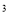 (y-x)
(y-x) 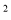 (x-y)+2(x-y)
(x-y)+2(x-y) 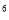
 把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论:
把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论: