题目内容
10.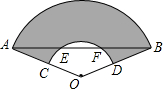 如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.
如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.
分析 过点O作OH⊥AB于点H,利用垂径定理和解直角△AHO求得AO的长度,然后根据扇形面积的计算公式进行解答.
解答  解:如图,过点O作OH⊥AB于点H,连接EO.
解:如图,过点O作OH⊥AB于点H,连接EO.
∵AE=20,EF=4,
∴AH=22.
由勾股定理可知OA2-AH2=OH2=OE2-EH2,
又OE=OC,即得OA2-OC2=AH2-EH2=484-4=480,
故阴影部分面积为S=$\frac{120π(O{A}^{2}-O{C}^{2})}{360}$=160π.
故答案是:160π.
点评 本题考查了扇形面积的计算,垂径定理以及解直角三角形的应用.熟记扇形面积公式是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.下列二次根式有意义的范围为x≥2的是( )
| A. | $\sqrt{\frac{1}{x-2}}$ | B. | $\sqrt{x-2}$ | C. | $\sqrt{\frac{1}{x+2}}$ | D. | $\sqrt{x+2}$ |
2.将点A(-3,3)向左平移3个单位长度,再向上平移5个单位长度则平移后点的坐标是( )
| A. | (0,8) | B. | (-6,-2) | C. | (0,-2) | D. | (-6,8) |

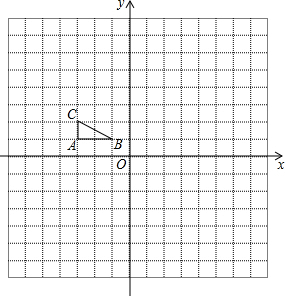 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
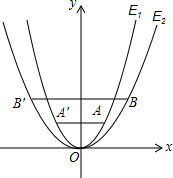 如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.