题目内容
5.学校计划选购甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书单价比乙种图书贵4元,用3000元购进甲种图书的数量与用2400元购进乙种图书的数量相同.(1)甲、乙两种图书的单价分别为多少元?
(2)学校计划购买这两种图书共100本,请求出所需经费W(单位:元)与购买甲种图书m(单位:本)之间的函数关系式;
(3)在(2)的条件下,要使投入的经费不超过1820元,且使购买的甲种图书的数量不少于乙种图书数量,则共有几种购买方案?
分析 (1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据:3000元购进甲种图书的数量=2400元购进乙种图书的数量相同列出方程求解即可;
(2)购买甲种图书m,则购买乙图书(100-m)本,根据:所需经费=甲图书总费用+乙图书总费用可列函数关系式;
(3)根据:总经费W≤1820且购买的甲种图书的数量≥乙种图书数量列出不等式组,解不等式组即可的不等式组的解集,从而确定方案.
解答 解:(1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据题意,
得:$\frac{3000}{x}=\frac{2400}{x-4}$,
解得:x=20,
经检验x=20是原方程的根,
则x-4=16,
答:甲图书的单价为20元/本,则乙图书的单价为16元/本.
(2)购买甲种图书m,则购买乙图书(100-m)本,根据题意,
有:W=20m+16(100-m)=4m+1600;
(3)根据题意,得:$\left\{\begin{array}{l}{4m+1600≤1820}\\{m≥100-m}\end{array}\right.$,
解得:50≤m≤55,
∵m需取整数,
∴m的值可以是:50,51,52,53,54,55,
故购买方案有6种:①甲图书50本,乙图书50本;②甲图书51本,乙图书49本;③甲图书52本,乙图书48本;④甲图书53本,乙图书47本;⑤甲图书54本,乙图书46本;⑥甲图书55本,乙图书45本.
点评 本题主要考查分式方程、一次函数、不等式组的综合应用能力,根据题意准确抓住相等关系或不等关系是解题的根本和关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
15.下列运算正确的是( )
| A. | a3•a4=a12 | B. | a3÷a3=0 | C. | a3+a3=2a6 | D. | 3a2•5a3=15a5 |
20.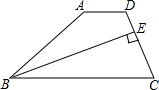 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )| A. | $\frac{7}{4}$ | B. | $\frac{5}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
 如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.
如图,点P是正方形ABCD的对角线BD上的一点,连接CP并延长,交AD于E,交BA的延长线于点F.若PE=4,EF=5,则线段PC的长为6.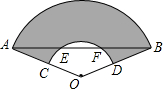 如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.
如图是一把折扇,∠O=120°,AB交$\widehat{CD}$于点E,F,已知AE=20,EF=4,则扇面(阴影部分)的面积为160π.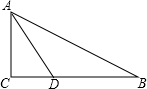 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.