题目内容
2.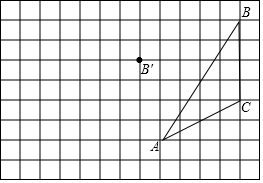 画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出△ABC中AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是:平行且相等;
(4)求四边形ACBB′的面积.
分析 (1)根据图形平移的性质画出△A′B′C′即可;
(2)根据方格的特点及高线的定义作出AB边上的中线CD和BC边上的高线AE即可;
(3)根据图形平移的性质即可得出结论;
(4)利用S四边形ACBB′=S长方形BEC’F-S△AEC-S△AC’B′-S△BFB′即可得出结论.
解答  解:(1)如图所示,△A′B′C′即为所求;
解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD,AE即为所求;
(3)∵△A′B′C′由△ABC平移而成,
∴线段AA′与线段BB′的关系是平行且相等.
故答案为:平行且相等;
(4)S四边形ACBB′=S长方形BEC’F-S△AEC-S△AC’B′-S△BFB′
=5×6-$\frac{1}{2}$×4×2-$\frac{1}{2}$×4×1-$\frac{1}{2}$×5×2
=30-4-2-5
=19.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.阅读可以增进人们的知识也能陶冶人们的情操.我们要多阅读,多阅读有营养的书.因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
请结合以上信息解答下列问题
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.
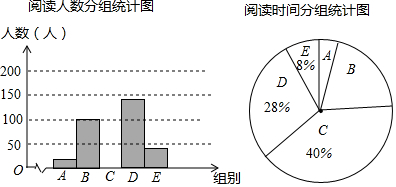
| 阅读时间分组统计表 | ||
| 组别 | 阅读时间x(h) | 人数 |
| A | 0≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | b |
| D | 30≤x<40 | 140 |
| E | x≥40 | c |
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.

7.等腰三角形一腰上的高于另一腰的夹角为50°,那么这个三角形的顶角为( )
| A. | 40° | B. | 100° | C. | 140° | D. | 40°或140° |
 如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=70°,∠C=45°,求∠EDC的度数.
如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=70°,∠C=45°,求∠EDC的度数. 在△ABC中,∠A:∠ABC:∠C=1:2:3,AB的垂直平分线分别交AB、AC于点D、E,求证:AE=2CE.
在△ABC中,∠A:∠ABC:∠C=1:2:3,AB的垂直平分线分别交AB、AC于点D、E,求证:AE=2CE.