题目内容
14. 在△ABC中,∠A:∠ABC:∠C=1:2:3,AB的垂直平分线分别交AB、AC于点D、E,求证:AE=2CE.
在△ABC中,∠A:∠ABC:∠C=1:2:3,AB的垂直平分线分别交AB、AC于点D、E,求证:AE=2CE.
分析 连接BE,根据线段垂直平分线的性质得到BE=AE,得到∠EBC=60°-30°=30°,根据直角三角形的性质即可得到结论.
解答  证明:连接BE,
证明:连接BE,
∵∠A:∠ABC:∠C=1:2:3,
∴∠A=$\frac{1}{6}$×180°=30°,∠ABC=2×30°=60°,∠C=3×30°=90°,
∵DE是AB 的垂直平分线,
∴BE=AE,
∴∠A=∠ABE=30°,
∴∠EBC=60°-30°=30°,
∴在Rt△BCE中,BE=2CE,
∵BE=AE,
∴AE=2CE.
点评 本题考查了线段的垂直平分线的性质,含30°角的直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若x2+2(m-3)x+16是完全平方式,则m的值等于( )
| A. | 3 | B. | -5 | C. | -7或1 | D. | 7或-1 |
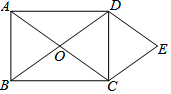 矩形ABCD对角线相交点O,DE∥AC,CE∥BD,若AD=4,CD=3,则四边形ODEC的面积为6.
矩形ABCD对角线相交点O,DE∥AC,CE∥BD,若AD=4,CD=3,则四边形ODEC的面积为6.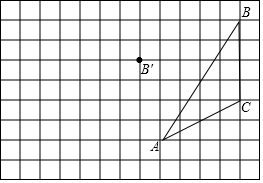 画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′. 如图,点E在四边形ABCD的边AD上,∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:AD=AE+AB.
如图,点E在四边形ABCD的边AD上,∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:AD=AE+AB.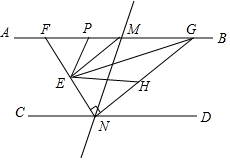 如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.