题目内容
15.小张在纸上随意写了两组连续自然数1,2,3,4,5,6,偶然发现2×4=32-12,5×4=62-42,于是她让同桌的小李也随意写了三个连续自然数,小李随意写出9,10,11.她们发现了10×4=112-92,这是一种巧合吗?她们猜想其中一定蕴含着某种规律,你能发现这个规律并用含某个字母的式子表示吗?试着用所学的知识说明你的猜想是正确的.分析 由2×4=32-12,5×4=62-42,…可以看出三个连续自然数,中间数的4倍是最大的自然数的平方减去最小自然数的平方,由此用字母表示并加以证明即可.
解答 解:假设三个连续自然数分别为n,n+1,n+2;
则4(n+1)=(n+2)2-n2.
理由:(n+2)2-n2
=n2+4n+4-n2
=4n+4
=4(n+1).
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用运算规律解决问题.

练习册系列答案
相关题目
4.在一个不透明的袋子中装有红、黄两种颜色的球共20个,每个球除颜色外完全相同.某学习兴趣小组做摸球实验,将球搅匀后从中随机摸出1个球,记下颜色后再放回袋中,不断重复.下表是活动进行中的部分统计数据.
(1)完成上表;
(2)“摸到红球”的概率的估计值是0.6(精确到0.1)
(3)试估算袋子中红球的个数.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
(2)“摸到红球”的概率的估计值是0.6(精确到0.1)
(3)试估算袋子中红球的个数.
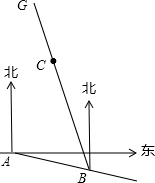 如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.
如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.



 如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.
如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.