题目内容
 已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=| m |
| x |
(1)求一次函数的解析式;
(2)若C(x1,y1),D(x2,y2),且x1•x2=-3,求反比例函数的解析式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由OA=OB=1,可得A、B的坐标,代入一次函数解析式可求得一次函数解析式;
(2)联立两函数解析式,消去y,得到一个关于x的一元二次方程,利用根与系数的关系可得到关于m的方程,求得m,即可求得反比例函数的解析式.
(2)联立两函数解析式,消去y,得到一个关于x的一元二次方程,利用根与系数的关系可得到关于m的方程,求得m,即可求得反比例函数的解析式.
解答:解:
(1)∵OA=OB=1,
∴A(-1,0),B(0,-1),
∵A、B两点在一次函数图象上,
∴代入一次函数解析式可得
,解得
,
∴一次函数解析式为y=-x-1;
(2)联立两函数解析式消去y可得:x2+x+m=0,
∵C、D是两函数图象的交点,
∴x1、x2是方程x2+x+m=0的两根,
∴x1•x2=m,又x1•x2=-3,
∴m=-3,
∴反比例函数解析式为y=-
.
(1)∵OA=OB=1,
∴A(-1,0),B(0,-1),
∵A、B两点在一次函数图象上,
∴代入一次函数解析式可得
|
|
∴一次函数解析式为y=-x-1;
(2)联立两函数解析式消去y可得:x2+x+m=0,
∵C、D是两函数图象的交点,
∴x1、x2是方程x2+x+m=0的两根,
∴x1•x2=m,又x1•x2=-3,
∴m=-3,
∴反比例函数解析式为y=-
| 3 |
| x |
点评:本题主要考查待定系数法求函数解析式,在(1)中注意把线段的长度化为点的坐标,在(2)中两交点的横坐标是所得到一元二次方程的两根是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 A、B、C都在格点上,且每个小正方的边长都为1.已知AC=5,求B到直线AC的垂线段距离.
A、B、C都在格点上,且每个小正方的边长都为1.已知AC=5,求B到直线AC的垂线段距离. 如图,OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线,则∠AOP与∠MON的大小上有何关系?请你写出你的推测,并简要说明理由.
如图,OM、ON、OP分别是∠AOB、∠BOC、∠AOC的平分线,则∠AOP与∠MON的大小上有何关系?请你写出你的推测,并简要说明理由.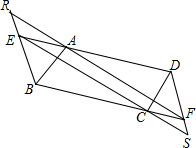 如图所示,在?ABCD中,E,F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S,求证:四边形RESF是平行四边形.
如图所示,在?ABCD中,E,F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S,求证:四边形RESF是平行四边形. 如图是一个包装纸盒的三视图(单位cm),则制作一个纸盒所需纸板的面积是多少?
如图是一个包装纸盒的三视图(单位cm),则制作一个纸盒所需纸板的面积是多少? 如图所示,△ABC中,AD是∠BAC的平分线,DE∥AB交AC于E,若AE:AC=2:5,则AB:AC=
如图所示,△ABC中,AD是∠BAC的平分线,DE∥AB交AC于E,若AE:AC=2:5,则AB:AC= 如图是一个几何体的三视图,则这个几何体的侧面积是
如图是一个几何体的三视图,则这个几何体的侧面积是 如图是一块从一个边长为50cm的正方形材料中裁出的垫片,现测量FG=8cm,求这个垫片的周长.
如图是一块从一个边长为50cm的正方形材料中裁出的垫片,现测量FG=8cm,求这个垫片的周长.