题目内容
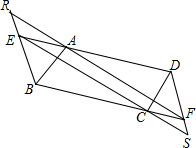 如图所示,在?ABCD中,E,F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S,求证:四边形RESF是平行四边形.
如图所示,在?ABCD中,E,F分别在DA、BC的延长线上,已知AE=CF,FA与BE的延长线相交于点R,EC与DF的延长线相交于点S,求证:四边形RESF是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:由在?ABCD中,AE=CF,易证得四边形BFDE是平行四边形,则可得BR∥DS,∠AEB=∠CFD,BE=DF,继而证得△AER≌△CFS(AAS),则可证得RE=FS,即可得BR=DS,则可证得四边形RESF是平行四边形.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BR∥DS,∠AEB=∠CFD,BE=DF,
∴∠R=∠S,∠AER=∠CFS,
在△AER和△CFS中,
,
∴△AER≌△CFS(AAS),
∴RE=FS,
∴BR=DS,
∴四边形RESF是平行四边形.
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BR∥DS,∠AEB=∠CFD,BE=DF,
∴∠R=∠S,∠AER=∠CFS,
在△AER和△CFS中,
|
∴△AER≌△CFS(AAS),
∴RE=FS,
∴BR=DS,
∴四边形RESF是平行四边形.
点评:此题考查了平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
| A、1:6 | B、1:8 |
| C、1:12 | D、1:16 |
 如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,
如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,| 3 |
如图所示是△ABC位似图形的几种画法,其中正确的是个数是( )


| A、1 | B、2 | C、3 | D、4 |
 已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= 如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.
如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,求∠AOD的度数.