题目内容
已知二次函数的对称轴是直线x=2,其最小值为5,各项系数和为6,求此抛物线与x轴交点的个数.
考点:抛物线与x轴的交点
专题:
分析:由条件可知其顶点坐标为(2,5),又各项系数和为6,可知过点(1,6),可求得二次函数的解析式,令y=0,得到一元二次方程,利用判别式可求得该方程的解的个数,则可求得抛物线线与x轴的交点个数.
解答:解:
∵对称轴是直线x=2,其最小值为5,
∴顶点坐标为(2,5),
∴可设二次函数解析式为y=a(x-2)2+5,
∵各项系数和为6,
∴二次函数图象过点(1,6),
代入可得a=1,
∴二次函数解析式为y=(x-2)2+5=x2-4x+9,
令y=0可得x2-4x+9=0,
其判别式△=16-36=-20<0,
∴方程x2-4x+9=0无实数解,
∴二次函数与x轴无交点.
∵对称轴是直线x=2,其最小值为5,
∴顶点坐标为(2,5),
∴可设二次函数解析式为y=a(x-2)2+5,
∵各项系数和为6,
∴二次函数图象过点(1,6),
代入可得a=1,
∴二次函数解析式为y=(x-2)2+5=x2-4x+9,
令y=0可得x2-4x+9=0,
其判别式△=16-36=-20<0,
∴方程x2-4x+9=0无实数解,
∴二次函数与x轴无交点.
点评:本题主要考查待定系数法求函数解析式及函数与x轴的交点,掌握二次函数的一般式、两点式、顶点式是解题的关键.注意二次函数与x轴的交点与一元二次方程的关系.

练习册系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
| A、1:6 | B、1:8 |
| C、1:12 | D、1:16 |
若∠A=12°12′,∠B=20°15′30″,∠C=20.25°,则( )
| A、∠A>∠B>∠C |
| B、∠B>∠C>∠A |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
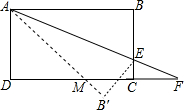 如图,在矩形ABCD中,AB=6cm,BC=3cm,点E是线段BC上的一个动点,连接AE并延长交DC延长线于点F,将△ABE沿直线AE翻折,点B落在B′处.线段AB′交CD于M点.当BE=2cm时,求DM.
如图,在矩形ABCD中,AB=6cm,BC=3cm,点E是线段BC上的一个动点,连接AE并延长交DC延长线于点F,将△ABE沿直线AE翻折,点B落在B′处.线段AB′交CD于M点.当BE=2cm时,求DM. 如图,△ABC的中线AE,BD相交于点G,DF∥BC交AE于点F,求
如图,△ABC的中线AE,BD相交于点G,DF∥BC交AE于点F,求 已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=