题目内容
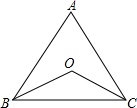 如图所示,∠ABO=∠ACO,BO=CO,试说明△ABC的形状.
如图所示,∠ABO=∠ACO,BO=CO,试说明△ABC的形状.考点:等腰三角形的判定与性质
专题:
分析:根据等边对等角可得∠OBC=∠OCB,然后结合已知条件求得∠ABC=∠ACB,最后根据等角对等边即可证得△ABC是等腰三角形.
解答:解:△ABC是等腰三角形;
∵BO=CO,
∴∠OBC=∠OCB,
∵∠ABO=∠ACO,
∴∠ABO+∠0BC=∠ACO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
∵BO=CO,
∴∠OBC=∠OCB,
∵∠ABO=∠ACO,
∴∠ABO+∠0BC=∠ACO+∠OCB,
即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
点评:本题考查了等腰三角形的判定与性质,是基础题,找出∠ABC=∠ACB的条件是解题的关键.

练习册系列答案
相关题目
下列判断正确的是( )
| A、四边形的外角和大于内角和 |
| B、一个多边形的内角和为1880° |
| C、一个多边形的内角中,锐角的个数可以任意多 |
| D、若多边形边数从3增加到n(n为大于3的自然数),它们的外角和度数不变 |
将△ABC的三个顶点坐标的横坐标乘以-1,纵坐标不变,则所得图形与原图形的关系是( )
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、绕原点旋转了180° |
| D、向x轴负方向平移了1个单位 |
下列各式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一次课堂练习,小张做了如下4道因式分解题,你认为小张做得不够完整的一题是( )
| A、x2-y2=(x+y)(x-y) |
| B、x2y-xy2=xy(x-y) |
| C、1-4x2=(1+2x)(1-2x) |
| D、x3-x=x(x2-1) |
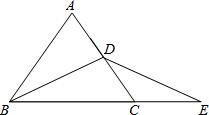 如图,在△ABC中,BA=BC,BD⊥AC,延长BC至点E,恰使CE=CD,BD=DE,求证:△ABC是等边三角形.
如图,在△ABC中,BA=BC,BD⊥AC,延长BC至点E,恰使CE=CD,BD=DE,求证:△ABC是等边三角形.