题目内容
已知⊙O的半径为1,PA为⊙O的切线,A为切点,且PA=1,弦AB=
,求PB的长.
| 2 |
考点:切线的性质
专题:
分析:先画图,再分两种情况:当弦AB与PA在O的同旁时;当弦AB与PA在O的两旁;分别讨论,即可得出答案.
解答:解:连接OA,
(1)如图1,当弦AB与PA在O的同旁时,
∵PA=AO=1,PA是⊙的切线,
∴∠PAO=90°,
∴∠APO=∠AOP=45°,
∴∠AOP=45°,
∵OA=OB,
∴∠BOP=∠AOP=45°,
而OP=OP,
∴△POA≌△POB,
∴PB=PA=1;
(2)如图2,当弦AB与PA在O的两旁,连接OA,OB,
∵PA是⊙O的切线,
∴OA⊥PA,
而PA=AO=1,
∴OP=
;
∵AB=
,
而OA=OB=1,
∴AO⊥BO,
∴四边形PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=
,
∴BC=
,
∴PB=
.
(1)如图1,当弦AB与PA在O的同旁时,

∵PA=AO=1,PA是⊙的切线,
∴∠PAO=90°,
∴∠APO=∠AOP=45°,
∴∠AOP=45°,
∵OA=OB,
∴∠BOP=∠AOP=45°,
而OP=OP,
∴△POA≌△POB,
∴PB=PA=1;
(2)如图2,当弦AB与PA在O的两旁,连接OA,OB,
∵PA是⊙O的切线,

∴OA⊥PA,
而PA=AO=1,
∴OP=
| 2 |
∵AB=
| 2 |
而OA=OB=1,
∴AO⊥BO,
∴四边形PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=
| 1 |
| 2 |
∴BC=
| ||
| 2 |
∴PB=
| 5 |
点评:本题考查了圆的切线,解题的关键是垂径定理与勾股定理的应用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
用一个底面大小为20cm×20cm的长方体容器(已装满水)向一个长、宽、高分别是8cm、5cm和10cm的长方体铁盒内倒水,当铁盒装满水时,长方体容器中水的高度下降了( )cm.
| A、2cm | B、0.5cm |
| C、1cm | D、2.5cm |
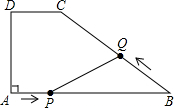 如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,AD:BC=3:5,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,AD:BC=3:5,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒. 如图,是一个很大很大的水域,现要测量A点和B点的距离,直接测量难度较大,你能设计一种简单的方法吗?请画图,写出已知、求证,并解释你的原理.
如图,是一个很大很大的水域,现要测量A点和B点的距离,直接测量难度较大,你能设计一种简单的方法吗?请画图,写出已知、求证,并解释你的原理.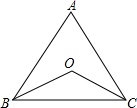 如图所示,∠ABO=∠ACO,BO=CO,试说明△ABC的形状.
如图所示,∠ABO=∠ACO,BO=CO,试说明△ABC的形状.