题目内容
若(a-1)4+|ab-3|=0,求
+
+
+…+
.
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+98)(b+98) |
考点:代数式求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:由条件可求得a=1,b=3,代入式子再利用裂项抵消法进行求解即可.
解答:解:由(a-1)4+|ab-3|=0,可得a=1,b=3,
所以原式=
+
+
+…+
+
=
×(
-
)+
×(
-
)+
×(
-
)+…+
×(
-
)+
×(
-
)
=
×(
-
+
-
+
-
+…+
-
+
-
)
=
×(1+
-
-
)
=
×
=
.
所以原式=
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 98×100 |
| 1 |
| 99×101 |
=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 98 |
| 1 |
| 100 |
| 1 |
| 2 |
| 1 |
| 99 |
| 1 |
| 101 |
=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 98 |
| 1 |
| 100 |
| 1 |
| 99 |
| 1 |
| 101 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 100 |
| 1 |
| 101 |
=
| 1 |
| 2 |
| 14949 |
| 10100 |
=
| 14949 |
| 20200 |
点评:本题主要考查非负数的性质及裂项抵消法,代入a、b的值代入后正确裂项是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用一个底面大小为20cm×20cm的长方体容器(已装满水)向一个长、宽、高分别是8cm、5cm和10cm的长方体铁盒内倒水,当铁盒装满水时,长方体容器中水的高度下降了( )cm.
| A、2cm | B、0.5cm |
| C、1cm | D、2.5cm |
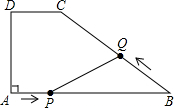 如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,AD:BC=3:5,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,AD:BC=3:5,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.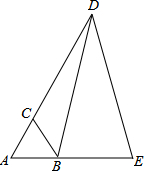 如图,等边△ABC,D、E分别在AC、AB的延长线上,且CD=AE,求证:BD=DE.
如图,等边△ABC,D、E分别在AC、AB的延长线上,且CD=AE,求证:BD=DE.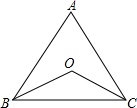 如图所示,∠ABO=∠ACO,BO=CO,试说明△ABC的形状.
如图所示,∠ABO=∠ACO,BO=CO,试说明△ABC的形状.