题目内容
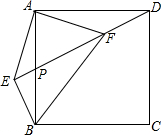 如图,正方形ABCD中,P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,过点A作AF⊥AE交DP于点F,连接BF.
如图,正方形ABCD中,P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,过点A作AF⊥AE交DP于点F,连接BF.(1)若AE=1,求EF的长;
(2)求证:PF=EP+EB.
考点:正方形的性质,全等三角形的判定与性质,勾股定理
专题:证明题
分析:(1)根据正方形的性质可得AB=AD,∠BAD=90°,然后求出∠BAE=∠DAF,再根据等角的余角相等求出∠ABE=∠ADF,再利用“角边角”证明△ABE和△ADF全等,根据全等三角形对应边相等可得AE=AF,从而得到△AEF是等腰直角三角形,根据等腰直角三角形的性质求解即可;
(2)过点A作AM⊥EF于M,根据等腰直角三角形的性质可得AM=MF=EM,根据线段中点定义可得AP=BP,然后利用“角角边”证明△AMP和△BEP全等,根据全等三角形对应边相等可得EP=PM,EB=AM,然后根据PF=PM+MF等量代换即可得证.
(2)过点A作AM⊥EF于M,根据等腰直角三角形的性质可得AM=MF=EM,根据线段中点定义可得AP=BP,然后利用“角角边”证明△AMP和△BEP全等,根据全等三角形对应边相等可得EP=PM,EB=AM,然后根据PF=PM+MF等量代换即可得证.
解答:(1)解:在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥AE,
∴∠BAE+∠BAF=90°,
∴∠BAE=∠DAF,
∵BE⊥DP,
∴∠ABE+∠BPE=90°,
又∵∠ADF+∠APD=90°,∠BPE=∠APD(对顶角相等),
∴∠ABE=∠ADF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF,
∴△AEF是等腰直角三角形,
∵AE=1,
∴EF=
AE=
×1=
;
(2)证明:过点A作AM⊥EF于M,
∵△AEF是等腰直角三角形,
∴AM=MF=EM,
∵P是AB的中点,
∴AP=BP,
在△AMP和△BEP中,
,
∴△AMP≌△BEP(AAS),
∴EP=PM,EB=AM,
∵PF=PM+MF,
∴PF=EP+EB.
∴∠DAF+∠BAF=90°,
∵AF⊥AE,
∴∠BAE+∠BAF=90°,
∴∠BAE=∠DAF,
∵BE⊥DP,
∴∠ABE+∠BPE=90°,
又∵∠ADF+∠APD=90°,∠BPE=∠APD(对顶角相等),
∴∠ABE=∠ADF,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(ASA),
∴AE=AF,
∴△AEF是等腰直角三角形,

∵AE=1,
∴EF=
| 2 |
| 2 |
| 2 |
(2)证明:过点A作AM⊥EF于M,
∵△AEF是等腰直角三角形,
∴AM=MF=EM,
∵P是AB的中点,
∴AP=BP,
在△AMP和△BEP中,
|
∴△AMP≌△BEP(AAS),
∴EP=PM,EB=AM,
∵PF=PM+MF,
∴PF=EP+EB.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理,熟记各性质与三角形全等的判定方法是解题的关键,(2)作辅助线构造成全等三角形是解题的关键.

练习册系列答案
相关题目

 如图,在平面直角坐标系中,已知△OAB的三个顶点分别为O(0,0)、A(8,6)、B(0,6),点P从点O出发在OA之间作往返运动,速度为每秒2个单位;点Q从O点出发在边OB、BA上沿O→B→A的方向运动,速度为每秒1个单位,当点Q到达终点A时,点P也停止运动.若P、Q两点同时出发,设运动的时间是t秒.
如图,在平面直角坐标系中,已知△OAB的三个顶点分别为O(0,0)、A(8,6)、B(0,6),点P从点O出发在OA之间作往返运动,速度为每秒2个单位;点Q从O点出发在边OB、BA上沿O→B→A的方向运动,速度为每秒1个单位,当点Q到达终点A时,点P也停止运动.若P、Q两点同时出发,设运动的时间是t秒.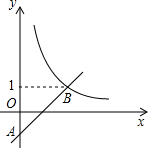 如图,在平面直角坐标系中,一次函数y=ax-a(a为常数)的图象与y轴相交于点A,与函数
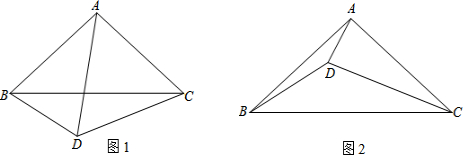
如图,在平面直角坐标系中,一次函数y=ax-a(a为常数)的图象与y轴相交于点A,与函数 如图,△ABC中,AB=AC,∠A=40°,点D为AC边上任意一点(不与点A、C重合),当△BCD为等腰三角形时,∠ABD的度数是
如图,△ABC中,AB=AC,∠A=40°,点D为AC边上任意一点(不与点A、C重合),当△BCD为等腰三角形时,∠ABD的度数是