题目内容
15.请你自己画图,写出已知,求证,证明“相似三角形对应角平分线之比等于相似比”.分析 画出图形,写出已知,求证,然后根据相似三角形对应角相等可得∠B=∠B1,∠BAC=∠B1A1C1,再根据角平分线的定义求出∠BAD=∠B1A1D1,然后利用两组角对应相等两三角形相似,根据相似三角形对应边成比例列式证明即可.
解答 已知:如图,已知△ABC∽△A1B1C1,顶点A、B、C分别与A1、B1、C1对应,△ABC和△A1B1C1的相似比为k,AD、A1D1分别是△ABC和△A1B1C1的角平分线.
求证:$\frac{AD}{{A}_{1}{D}_{1}}$=k;
证明:∵△ABC∽△A1B1C1,顶点A、B、C分别与A1、B1、C1对应,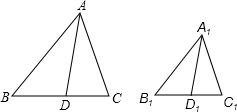
∴∠B=∠B1,∠BAC=∠B1A1C1,
∵AD、A1D1分别是△ABC,△A1B1C1的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAC,∠B1A1D1=$\frac{1}{2}$∠B1A1C1,
∴∠BAD=∠B1A1D1,
∴△ABD∽△A1B1D1,
∴$\frac{AD}{{A}_{1}{D}_{1}}$=$\frac{AB}{{A}_{1}{B}_{1}}$,
∴$\frac{AD}{{A}_{1}{D}_{1}}$=k,即相似三角形对应角平分线之比等于相似比.
点评 本题考查了相似三角形的性质与判定,主要利用了相似三角形对应角相等的性质,相似三角形对应边成比例的性质,以及两组角对应相等两三角形相似的判定方法,要注意文字叙述性命题的证明格式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
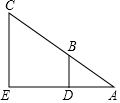 如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=12m,则河宽DE=6m.
如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=12m,则河宽DE=6m.