题目内容
19．若二次函数y=mx2+（m-2）x-1的图象与x轴的交点是A（a，0），B（b，0），且a+b=1，则有（ ）| A． | m=-1 | B． | m=1 | C． | m=2 | D． | 无法确定m的值 |
分析 图象与x轴的交点是A（a，0），B（b，0），则a和b是mx2+（m-2）x-1=0的解，利用一元二次方程根与系数的关系即可求解．
解答 解：根据题意得：a+b=-$\frac{m-2}{m}$=1，
解得：m=1．
故选B．
点评 本题考查了抛物线与x轴的交点，抛物线与x轴的交点的横坐标就是令函数y=0时，得到的一元二次方程的解．
练习册系列答案
名校课堂系列答案
相关题目
10．已知一元二次方程ax2-2x+1=0没有实数根，则抛物线y=ax2-2x+1的顶点所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
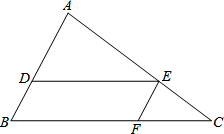如图，在△ABC中，DE∥BC，EF∥AB．
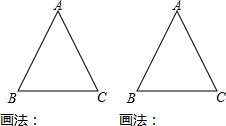晓明有一把没有刻度的直角三角板，他要用这块三角板找出一个等腰三角形的对称轴，你能帮他完成吗？请用两种方法在图中画出等腰三角形的对称轴并注明方法．
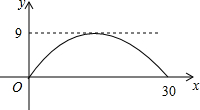有一座抛物线形拱桥，其最大高度为9m，现把它的示意图放在如图所示的平面直角坐标系中，则此抛物线的函数解析式为y=-$\frac{1}{25}$（x-15）2+9，其中自变量x的取值范围是0≤x≤30．
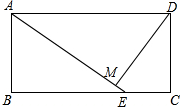如图，在矩形ABCD中，AB=3，BC=6，且BE=2EC，DM⊥AE于M．求sin∠MAD的值．
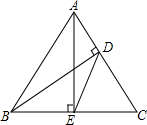如图，在△ABC中，AE、BD分别是边BC、AC上的高，且∠C=60°．