题目内容
16.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售4件,问:每件降价多少元时,才能使利润最大?最大利润是多少?分析 根据题意列出利润与降价的函数关系式,根据二次函数的性质解决问题.
解答 解:当每件衬衫降价x元时,每天可出售(4x+20)件,此时每件可盈利(45-x)元,设利润为y元.
∴y=(45-x)(4x+20)
=-4x2+160x+900
∵a=-4<0,所以上述抛物线开口向下,函数有最大值
当x=-$\frac{160}{2×(-4)}$=20时,y取得最大值,此时y=$\frac{4×(-4)×900-16{0}^{2}}{4×(-4)}$=2500元.
所以每件降价20元时,才能使利润最大,最大利润是2500元.
点评 此题主要考查了二次函数的应用,弄清题意,找出合适的等量关系,进而列出函数表达式是解答此类问题的关键,此题还考查了“配方法”在求函数的最大值的问题中的应用,要熟练掌握.

练习册系列答案
相关题目
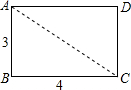 如图,一矩形纸片ABCD,用剪刀沿虚线AC将该纸片剪成两块三角形,现要用剪得的两块三角形拼接成一个等腰三角形,请设计两种不同的方法,并将两种拼法画在方框中,要求在图中标明用于拼接的直角三角形的三边长.
如图,一矩形纸片ABCD,用剪刀沿虚线AC将该纸片剪成两块三角形,现要用剪得的两块三角形拼接成一个等腰三角形,请设计两种不同的方法,并将两种拼法画在方框中,要求在图中标明用于拼接的直角三角形的三边长.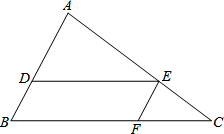 如图,在△ABC中,DE∥BC,EF∥AB.
如图,在△ABC中,DE∥BC,EF∥AB.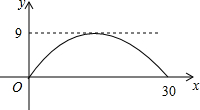 有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.
有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.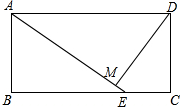 如图,在矩形ABCD中,AB=3,BC=6,且BE=2EC,DM⊥AE于M.求sin∠MAD的值.
如图,在矩形ABCD中,AB=3,BC=6,且BE=2EC,DM⊥AE于M.求sin∠MAD的值.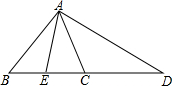 如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.
如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.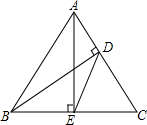 如图,在△ABC中,AE、BD分别是边BC、AC上的高,且∠C=60°.
如图,在△ABC中,AE、BD分别是边BC、AC上的高,且∠C=60°. 已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.