题目内容
10.关于x的方程$\frac{4-ax}{x+2}$=3的解为非正数,则a的取值范围是( )| A. | a>-3 | B. | a≥-3 | C. | a>-3且a≠-2 | D. | a<-3 |
分析 先解一元一次方程$\frac{4-ax}{x+2}$=3得到x=-$\frac{2}{3+a}$,利用解为非正数得到-$\frac{2}{a+3}$≤0,然后解此不等式即可.
解答 解:解方程$\frac{4-ax}{x+2}$=3得x=-$\frac{2}{a+3}$,
∵关于x的方程$\frac{4-ax}{x+2}$=3的解为非正数,
∴-$\frac{2}{a+3}$<0,
解得:a>-3且a≠-2.
故选C.
点评 此题考查了分式方程的解,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若以三个数为三角形三边的长能构成直角三角形,我们就把它们称为一组勾股数,如3,4,5,勾股数之间存在一种奇妙的联系,观察下表,结合表中数的规律及相关知识,求出b,c的值
| 举例 | 猜 想 |
| 5、12、13 | 52=12+13 |
| 7、24、25 | 72=24+25 |
| … | … |
| 13、b、c | 132=b+c |
 如图.在Rt△ABC中,∠C=90°,BC=$\sqrt{3}$,CD⊥AB,垂足为D,AD=2,求AB的长和tanA的值.
如图.在Rt△ABC中,∠C=90°,BC=$\sqrt{3}$,CD⊥AB,垂足为D,AD=2,求AB的长和tanA的值.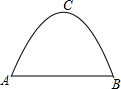 如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.
如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.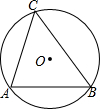 已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.
已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.