题目内容
15.寻求某些勾股数的规律:(1)对于任何一组已知的勾股数都扩大相同的正整数倍后,就得到了一组新的勾股数.例如:32+42=52,若把它扩大2倍、3倍,就分别得到62+82=102和92+122=152,…若把它扩大11倍,就得到332+442=552,若把它扩大n倍(n为正整数),就得到(3n)2+(4n)2=(5n)2.
(2)对于任意一个大于1的奇数,存在着下列勾股数:
若勾股数为3,4,5,因为32=52-42,则有32=4+5;
若勾股数为5,12,13,则有52=12+13;
若勾股数为7,24,25,则有72=24+25;…
若勾股数为17,a,b(a<b),根据以上的规律,求a、b的值.
分析 (1)根据已知数据找出规律进而得出答案;
(2)把已知数据代入经过证明成立的规律即可得出答案.
解答 解:(1)∵32+42=52,把它扩大2倍、3倍,就分别得到62+82=102和92+122=152,…
∴把它扩大11倍,就得到332+442=552,若把它扩大n倍(n为正整数),就得到(3n)2+(4n)2=(5n)2.
故答案为:332+442=552,(3n)2+(4n)2=(5n)2;
(2)∵32=9=4+5,52=25=12+13,…
∴72=49=24+25,
由以上特点我们可猜想并证明这样一个结论:设m为大于1的奇数,将m2拆分为两个连续的整数之和,
即m2=n+(n+1),则m,n,n+1就构成一组简单的勾股数,
证明:∵m2=n+(n+1)(m为大于1的奇数),∴m2+n2=2n+1+n2=(n+1)2,∴m,n,(n+1)是一组勾股数;
运用以上结论,∵172=289=144+145,∴a=144,b=145.
故答案为:72=49=24+25.
点评 此题主要考查了勾股数,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在讨论方程$\frac{x}{x+3}$=$\frac{-3}{x+3}$的解的情况时,四位同学有下列四种不同的看法,你认为正确的是( )
| A. | 无解 | B. | 解为x=-3 | C. | 解为任意数 | D. | 不能确定 |
10.关于x的方程$\frac{4-ax}{x+2}$=3的解为非正数,则a的取值范围是( )
| A. | a>-3 | B. | a≥-3 | C. | a>-3且a≠-2 | D. | a<-3 |
20.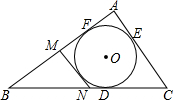 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
 如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )
如图,⊙O是△ABC的内切圆,D、E、F为切点,AB=18cm,BC=20cm,AC=12cm,MN切⊙O交AB于M,交BC于N,则△BNN的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
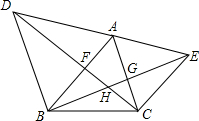 如图,△ABC中,∠A=60°,分别以AB、AC为边作等边△ABD、等边△ACE,连CD交AB于F,连BE交AC于G,CD、BE交于H点,在不添加辅助线的情况下,从图形中找出三组全等三角形,并选其中的两组进行证明.
如图,△ABC中,∠A=60°,分别以AB、AC为边作等边△ABD、等边△ACE,连CD交AB于F,连BE交AC于G,CD、BE交于H点,在不添加辅助线的情况下,从图形中找出三组全等三角形,并选其中的两组进行证明.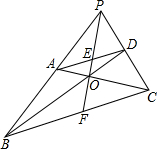 已知:如图,AD∥BC,BD、AC交于O,BA、CD的延长线交于P,PO的延长线交BC于F.求证:
已知:如图,AD∥BC,BD、AC交于O,BA、CD的延长线交于P,PO的延长线交BC于F.求证: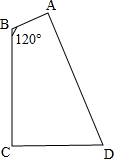 已知如图,四边形ABCD中,BC⊥CD,BA⊥AD,BA=2,AD=20,∠ABC=120°,求BC的长.
已知如图,四边形ABCD中,BC⊥CD,BA⊥AD,BA=2,AD=20,∠ABC=120°,求BC的长.