题目内容
2．
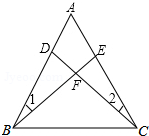如图，在△ABC中，已知∠1=∠2，BE=CD，AB=7，AE=3，则CE=4．
分析 由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．
解答 解：在△ABE和△ACD中，
$\left\{\begin{array}{l}{∠1=∠2}\\{∠A=∠A}\\{BE=CD}\end{array}\right.$，
∴△ABE≌△ACD（AAS），
∴AD=AE=3，AC=AB=7，
∴CE=BD=AB-AD=4，
故答案为：4．
点评 本题主要考查了全等三角形的性质和判定，熟记全等三角形的判定方法是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
12．下列各式中，计算正确的是（ ）
| A． | （2a+b）2=4a2+b2 | B． | （-a+b）（a-b）=a2-b2 | ||
| C． | （$\frac{1}{2}$x+1）（-$\frac{1}{2}$x-1）=$\frac{1}{4}$x2-1 | D． | （-x-y）2=x2+2xy+y2 |
13．下列命题中，假命题是（ ）
| A． | 若点B在线段AC上，且AB2=AC•BC，那么点B是线段AC的黄金分割点 | |
| B． | 位似图形一定是相似图形 | |
| C． | 各角对应相等的两个多边形是相似多边形 | |
| D． | 两个全等三角形的相似比等于面积比 |
10．圆锥的底面半径为r，母线为l，当r=1，l=3时，圆锥的侧面展开的扇形面积为（ ）
| A． | π | B． | 3π | C． | 9π | D． | 2$\sqrt{2}$π |
17．
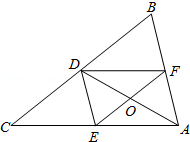如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．结论正确的是（ ）
如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．结论正确的是（ ）| A． | 0A=0D | B． | EF=DF | C． | AF=AE | D． | BD=DE |
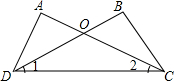题目：如图，已知AC，BD相交于点0．∠A=∠B，∠1=∠2，试说明△AOD≌△BOC．