题目内容
17. 已知,如图,直角△ABC中,∠C=90°
已知,如图,直角△ABC中,∠C=90°(1)在△ABC内画正方形DEFG,使得点D在AB上,E在BC上,F、G在AC上(不写画法,保留画图痕迹);
(2)若BC=4,AC=6,求出(1)中所画的正方形的边长.
分析 (1)如图,过点C作∠C的平分线CD,作DE⊥BC于E,DF⊥AC于F.四边形DECF即为所求.
(2)设正方形边长为x,由DE∥AC,推出△BDE∽△BAC,得$\frac{DE}{AC}$=$\frac{BE}{BC}$,列出方程即可解决问题.
解答 解:(1)如图,过点C作∠C的平分线CD,作DE⊥BC于E,DF⊥AC于F.
四边形DECF即为所求.
(2)设正方形边长为x,
∵DE∥AC,
∴△BDE∽△BAC,
∴$\frac{DE}{AC}$=$\frac{BE}{BC}$,
即$\frac{x}{6}$=$\frac{4-x}{4}$,
∴x=2.4
∴正方形的边长为2.4.
点评 本题考查作图-复杂作图、正方形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7. 已知a,b在数轴上的位置如图,则下列式子正确的是( )
已知a,b在数轴上的位置如图,则下列式子正确的是( )
 已知a,b在数轴上的位置如图,则下列式子正确的是( )
已知a,b在数轴上的位置如图,则下列式子正确的是( )| A. | a-b>a | B. | |a|<b-a | C. | b-a<a-b | D. | -a<b |
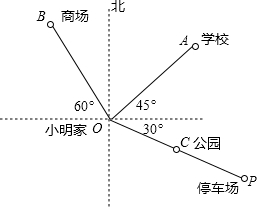 如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.
如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点. 证明“三角形的外角和等于360°”.
证明“三角形的外角和等于360°”.
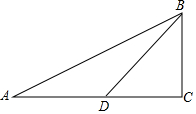 在Rt△ABC中,∠ACB=90°,D是AC上一点,∠A=α,∠ABD=β,若tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,求:tan(α+β)的值.
在Rt△ABC中,∠ACB=90°,D是AC上一点,∠A=α,∠ABD=β,若tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,求:tan(α+β)的值.