题目内容
6.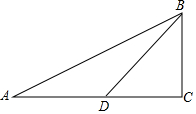 在Rt△ABC中,∠ACB=90°,D是AC上一点,∠A=α,∠ABD=β,若tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,求:tan(α+β)的值.
在Rt△ABC中,∠ACB=90°,D是AC上一点,∠A=α,∠ABD=β,若tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$,求:tan(α+β)的值.
分析 作DE⊥AB于点E,由tanα=$\frac{DE}{AE}$=$\frac{1}{2}$、tanβ=$\frac{DE}{BE}$=$\frac{1}{3}$设DE=x,则AE=2x,BE=3x,AB=5x,根据勾股定理求得AD=$\sqrt{5}$x、BD=$\sqrt{10}$x,再证△ADE∽△ABC得$\frac{DE}{BC}=\frac{AD}{AB}$,即$\frac{x}{BC}=\frac{\sqrt{5}x}{5x}$,从而求出BC=$\sqrt{5}$x,根据勾股定理求得DC=$\sqrt{5}$x,即可得答案.
解答 解:如图,作DE⊥AB于点E,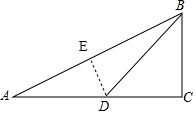
则∠AED=∠BED=90°,
∵tanα=$\frac{DE}{AE}$=$\frac{1}{2}$,tanβ=$\frac{DE}{BE}$=$\frac{1}{3}$,
∴设DE=x,则AE=2x,BE=3x,
∴AB=5x,
由勾股定理可得AD=$\sqrt{5}$x,BD=$\sqrt{10}$x,
∵∠AED=∠C=90°,∠A=∠A,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AD}{AB}$,即$\frac{x}{BC}=\frac{\sqrt{5}x}{5x}$,
解得:BC=$\sqrt{5}$x,
由勾股定理可得DC=$\sqrt{B{D}^{2}-B{C}^{2}}$=$\sqrt{(\sqrt{10}x)^{2}-(\sqrt{5}x)^{2}}$=$\sqrt{5}$x,
∴tan(α+β)=tan∠ADC=$\frac{BC}{DC}$=$\frac{\sqrt{5}x}{\sqrt{5}x}$=1.
点评 本题主要考查解直角三角形的应用,熟练掌握三角函数的定义,结合题意建立合适的直角三角形并表示出所需边的长度是解题的关键.

(1)试完成表格:
| 姓名 | 小颖 | 小明 | 小刚 | 小京 | 小宁 |
| 体重(千克) | 34 | 44 | 45 | 37 | 41 |
| 体重与平均体重的差 | -7 | +3 | +4 | -4 | 0 |
(3)最重的与最轻的相差多少?
| A. | a=1 | B. | a≠1 | C. | a≠-1 | D. | a≠0且b≠0 |
| A. | 13 | B. | 2 | C. | 17 | D. | -7 |
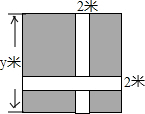 如图,小区在边长为y米的正方形内,修宽为2米的通道,其余部分种草.
如图,小区在边长为y米的正方形内,修宽为2米的通道,其余部分种草. 已知,如图,直角△ABC中,∠C=90°
已知,如图,直角△ABC中,∠C=90° 如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.
如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5. 如图,已知AB为⊙O的弦,从圆上任一点引弦CD⊥AB,作∠OCD的平分线交⊙O于点P,连接PA、PB,求证:PA=PB.
如图,已知AB为⊙O的弦,从圆上任一点引弦CD⊥AB,作∠OCD的平分线交⊙O于点P,连接PA、PB,求证:PA=PB.