题目内容
16．已知两个正多边形，其中一个正多边形的外角是另一个正多边形外角的2倍，并且用这两个正多边形可以拼成平面图形，求这两个正多边形的边数．分析 根据n边形内角和公式和多边形内角与外角可求n边形每个外角的度数，再根据平面镶嵌的特征即可求解．
解答 解：n边形内角和为180°×（n-2），
每个外角就是180°-$\frac{180°×（n-2）}{n}$=$\frac{360°}{n}$，
两个多边形又能拼成平面图形，
所以一个的内角等于另一个的外角，
所以一个是6边形，一个是三角形．
点评 考查了多边形内角与外角，平面镶嵌问题，关键是得到n边形每个外角的度数．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB=4，求：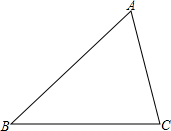
如图，△ABC，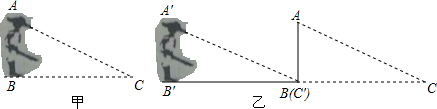
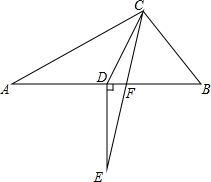已知：在△ABC中，∠ACB=90°，CF是∠ACB的交平分线，点D在边AB上，∠ACD=∠A，ED⊥AB交CF的延长线于点E，求证：∠E=∠DCF．