题目内容
2.已知:M点是等边三角形△ABC中BC边上的中点,也是等边△DEF中EF边上的中点,连结AD.(1)如图1,当EF与BC在同一条直线上时,直接写出$\frac{AD}{BE}$的值;
(2)如图2,△ABC固定不动,将图1中的△DEF绕点M顺时针旋转α(0°≤α≤90°)角,
①判断(1)中的结论是否仍然成立,若成立,请加以证明;若不成立,说明理由;
②作DH⊥BC于点H.设BH=x,线段AB,BE,ED,DA所围成的图形面积为S.当AB=6,DE=2时,求S关于x的函数关系式,并写出相应的x的取值范围.

分析 (1)作DG⊥AB于点G,作EH⊥AB于点H.则四边形DGHE是矩形,则在直角△ADG和直角△BEH中,利用x表示出AD和BE的长,即可求得数量关系;
(2)①连接DM,AM,然后证明△ADM∽△BEM,即可证得结论;②分(Ⅰ)当△DEF绕点M顺时针旋转α(0°≤α≤90°)角,根据△ADM∽△BEM,利用相似三角形的面积的比等于相似比的平方,以及面积的和差即可求得函数的解析式.
解答 解:(1)作DG⊥AB于点G,作EH⊥AB于点H.则四边形DGHE是矩形(如图1),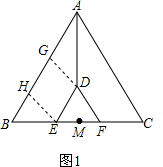
设DG=HE=x,
在直角△ADG中,AD=$\frac{DG}{sin30°}$=2x,
在直角△BEH中,BE=$\frac{HE}{sin60°}$=$\frac{2x}{\sqrt{3}}$,
则$\frac{AD}{BE}$=$\sqrt{3}$.
(2)①存在,证明:连接DM,AM.
在等边三角形ABC中,M为BC的中点,
∴AM⊥BC,∠BAM=$\frac{1}{2}$∠BAC=30°,$\frac{AM}{BM}$=$\sqrt{3}$.
∴∠BME+∠EMA=90°.
同理,$\frac{DM}{EM}$=$\sqrt{3}$,∠AMD+∠EMA=90°.
∴$\frac{AM}{BM}$=$\frac{DM}{EM}$,∠AMD=∠BME.
∴△ADM∽△BEM.
∴$\frac{AD}{BE}$=$\frac{DM}{EM}$=$\sqrt{3}$.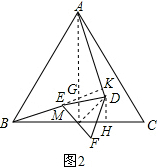
当△DEF绕点M顺时针旋转α(0°≤α≤90°)角时,(如图2),
∵△ADM∽△BEM,
∴$\frac{{S}_{△ADM}}{{S}_{△BEM}}$=($\frac{AD}{BE}$)2=3.
∴S△BEM=$\frac{1}{3}$S△ADM
∴S=S△ABM+S△ADM-S△BEM-S△DEM
=S△ABM+$\frac{2}{3}$S△ADM-S△DEM
=$\frac{1}{2}$×3×3$\sqrt{3}$+$\frac{2}{3}$×$\frac{1}{2}$×3$\sqrt{3}$(x-3)-$\frac{1}{2}$×1×$\sqrt{3}$
=$\sqrt{3}$x+$\sqrt{3}$.
∴s=$\sqrt{3}$x+$\sqrt{3}$ (3≤x≤3+$\sqrt{3}$).
点评 本题考查了相似三角形的判定与性质,矩形的性质,等边三角形的性质,正确作出辅助线,求得函数的解析式是关键.

(1)若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求购进的甲、乙两种商品各多少件?
(2)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
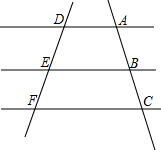 如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.
如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由. 如图所示,A、B是笔直公路l同侧的两个村庄,且两个村庄到公路l的距离分别是300m和500m,两村庄之间的距离为600m,现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?
如图所示,A、B是笔直公路l同侧的两个村庄,且两个村庄到公路l的距离分别是300m和500m,两村庄之间的距离为600m,现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?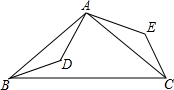 已知:AB=AC,AD=AE,BD=CE,求证:∠BAC=∠DAE.
已知:AB=AC,AD=AE,BD=CE,求证:∠BAC=∠DAE.