题目内容
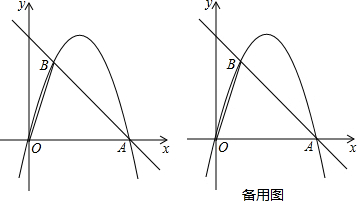
7. 如图所示,A、B是笔直公路l同侧的两个村庄,且两个村庄到公路l的距离分别是300m和500m,两村庄之间的距离为600m,现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?
如图所示,A、B是笔直公路l同侧的两个村庄,且两个村庄到公路l的距离分别是300m和500m,两村庄之间的距离为600m,现要在公路上建一汽车停靠站,使两村到停靠站的距离之和最小,问最小值是多少?
分析 根据轴对称求最短路线的方法得出停靠站C点位置,进而利用勾股定理求出答案.
解答  解:如图所示:作A点关于直线l的对称点,过点B作BD⊥l,过点A作AE⊥BD于点E,连接A′B,交直线l于点C,连接AC,BC,
解:如图所示:作A点关于直线l的对称点,过点B作BD⊥l,过点A作AE⊥BD于点E,连接A′B,交直线l于点C,连接AC,BC,
则AC+BC=A′C+BC此时最小,
由题意可得:AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{60{0}^{2}-20{0}^{2}}$=400$\sqrt{2}$(m),
则A′B=$\sqrt{A′{D}^{2}+B{D}^{2}}$=$\sqrt{320000+80{0}^{2}}$=400$\sqrt{6}$(m),
答:两村到停靠站的距离之和最小值是400$\sqrt{6}$m.
点评 此题主要考查了利用轴对称求最短路线,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
3.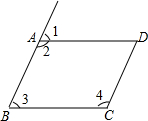 如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )
如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )
 如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )
如图,在四边形ABCD中,AB∥CD,AD∥BC,下列各式不一定正确的是( )| A. | ∠1+∠2=180° | B. | ∠2+∠3=180° | C. | ∠3+∠4=180° | D. | ∠2+∠4=180° |