题目内容
 如图,OA⊥OB,OC⊥OD,垂足为O,∠AOC
如图,OA⊥OB,OC⊥OD,垂足为O,∠AOC考点:余角和补角
专题:
分析:根据垂直,可得∠是90°,根据等式的性质,可得答案.
解答:解:∵OA⊥OB,OC⊥OD,垂足为O,
∴∠AOB=∠COD=90°.
∵∠AOB+BOC=∠COD+∠BOC,
∴∠AOC=∠BOD.
故答案为:=,等式的性质.
∴∠AOB=∠COD=90°.
∵∠AOB+BOC=∠COD+∠BOC,
∴∠AOC=∠BOD.
故答案为:=,等式的性质.
点评:本题考查了余角和补角,先根据垂直得出两角相等,根据等式的性质,得出答案.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若a2+3ab+b2+A=(a-b)2,则A是( )
| A、-2ab | B、-5ab |
| C、ab | D、-3ab |
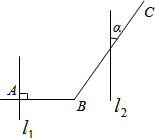 如图,已知
如图,已知 如图,下列结论正确的有( )
如图,下列结论正确的有( )