题目内容
2.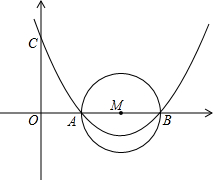 如图所示,已知M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于点A、B,抛物线y=$\frac{1}{6}$x2+bx+c过A、B两点且与y轴交于点C.
如图所示,已知M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于点A、B,抛物线y=$\frac{1}{6}$x2+bx+c过A、B两点且与y轴交于点C.(1)求点C的坐标;
(2)已知点Q(8,m)为抛物线上一点,点P为抛物线对称轴上一动点,求出P点坐标使得PQ+PB值最小,并求出最小值;
(3)过C点作⊙M的切线CE,求直线OE的解析式.
分析 (1)根据题意可知点A,B的坐标分别为(2,0),(6,0),代入函数解析式即可求得抛物线的解析式,即可得点C的坐标;
(2)根据图象可得PQ+PB的最小值即是AQ的长,所以抛物线对称轴l是x=4.所以Q(8,m)抛物线上,得到m=2.过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,求的AQ的值即可;
(3)此题首先要证得OE∥CM,利用待定系数法求得CM的解析式,即可求得OE的解析式.
解答 解:(1)由已知,得A(2,0),B(6,0),
∵抛物线y=$\frac{1}{6}$x2+bx+c过点A和B,
∴$\left\{\begin{array}{l}{\frac{1}{6}×{2}^{2}+b+c=0}\\{\frac{1}{6}×{2}^{2}+6b+c=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{b=-\frac{4}{3}}\\{c=2}\end{array}\right.$
则抛物线的解析式为
y=$\frac{1}{6}$x2-$\frac{4}{3}$x+2.
故C(0,2).
(2)如图,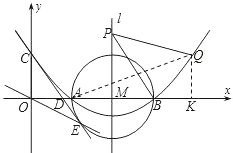
抛物线对称轴l是x=4.
∵Q(8,m)在抛物线上,
∴m=2.
过点Q作QK⊥x轴于点K,
则K(8,0),QK=2,AK=6,
∴AQ=$\sqrt{A{K}^{2}+Q{K}^{2}}$=2$\sqrt{10}$,
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=2$\sqrt{10}$.
(3)如图,
①连接EM和CM
由已知,得EM=OC=2.
∵CE是⊙M的切线,
∴∠DEM=90°,
则∠DEM=∠DOC.
又∵∠ODC=∠EDM.
∴△DEM≌△DOC.
∴OD=DE,CD=MD.
又在△ODE和△MDC中,∠ODE=∠MDC,∠DOE=∠DEO=∠DCM=∠DMC.
则OE∥CM.
设CM所在直线的解析式为y=kx+b,CM过点C(0,2),M(4,0),
∴$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$
∴$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$
∴直线CM的解析式为y=-$\frac{1}{2}$x+2,
又∵直线OE过原点O,且OE∥CM,
∴OE的解析式为y=-$\frac{1}{2}$x.
②如图,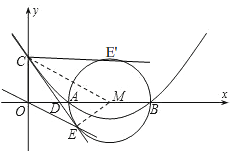
连接ME',
∴ME'⊥CE'
由(1)知,ME=OC=2,
∴CE'∥x轴,
∵C(0,2),M(4,0),
∴E'(4,2),
∴直线OE'的解析式为y=$\frac{1}{2}$x
点评 此题考查了二次函数与一次函数以及圆的综合知识,要注意待定系数法求解析式以及数形结合思想的应用.

 名校课堂系列答案
名校课堂系列答案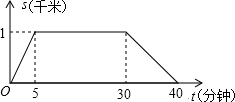 某天早晨,小明去体育馆晨练,如图是他离家的距离S(千米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是( )
某天早晨,小明去体育馆晨练,如图是他离家的距离S(千米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是( )| A. | 小明去时所用的时间多于回家所用的时间 | |
| B. | 小明在体育馆锻炼了30分钟 | |
| C. | 小明去时的速度大于回家的速度 | |
| D. | 小明去时走上坡路,回家时走下坡路 |
 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
| A. | 7 | B. | 8 | C. | 7或8 | D. | 无法确定 |

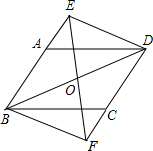 如图,在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交BA、DC的延长线于点E、F,且AE=CF,连接DE、BF.
如图,在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交BA、DC的延长线于点E、F,且AE=CF,连接DE、BF. 如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.
如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.