题目内容
13.方程组$\left\{\begin{array}{l}{(x-7)(x+8)=0}\\{\sqrt{2}x-\frac{1}{2}y=1}\end{array}\right.$共有2组解.分析 根据方程组的第一个方程求出x的值,把x的值代入第二个方程求出y的值,即可得出答案.
解答 解:$\left\{\begin{array}{l}{(x-7)(x-8)=0①}\\{\sqrt{2}x-\frac{1}{2}y=1②}\end{array}\right.$,$\left\{\begin{array}{l}{(x-7)(x+8)=0①}\\{\sqrt{2}x-\frac{1}{2}y=1②}\end{array}\right.$
由①得:x-7=0,x+8=0,
解得:x1=7,x2=-8,
把x=7代入①得:y=14$\sqrt{2}$-2,
把x=-8代入①得:y=-16$\sqrt{2}$-2,
即方程组有2组解,
故答案为:2.
点评 本题考查了解一元二次方程和解二元一次方程组的应用,能求出x的值是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知一个直角三角形的两条边长分别是6和8,则第三边长是( )
| A. | 10 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10或2$\sqrt{7}$ |
18.在下列说法中,正确的有( )
①两点确定一条直线;
②过一点有且只有一条直线与已知直线平行;
③垂直于同一条直线的两条直线垂直;
④平行于同一条直线的两条直线平行;
⑤过一点有且只有一条直线和已知直线垂直.
①两点确定一条直线;
②过一点有且只有一条直线与已知直线平行;
③垂直于同一条直线的两条直线垂直;
④平行于同一条直线的两条直线平行;
⑤过一点有且只有一条直线和已知直线垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3. 如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )
如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )
 如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )
如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )| A. | ∠AEF=∠EFD | B. | AB∥GH | C. | ∠BEF=∠EGH | D. | GH∥CD |
 如图,将三角板的直角顶点放在直尺的一边上,若∠1=70°,则∠2的度数为20°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=70°,则∠2的度数为20°.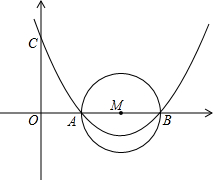 如图所示,已知M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于点A、B,抛物线y=$\frac{1}{6}$x2+bx+c过A、B两点且与y轴交于点C.
如图所示,已知M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于点A、B,抛物线y=$\frac{1}{6}$x2+bx+c过A、B两点且与y轴交于点C.