题目内容
3.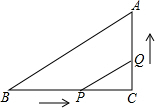 如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?
如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?
分析 设经过y秒后相似,由于没有说明对应角的关系,所以共有两种情况:△CPQ∽△CBA与△CPQ∽△CAB
解答 解:设经过y秒后,△CPQ∽△CBA,此时BP=2y,CQ=y.
∵CP=BC-BP=8-2y,CB=8,CQ=y,CA=6.
∵△CPQ∽△CBA,
∴$\frac{CP}{CB}=\frac{CQ}{CA}$,
∴$\frac{8-2y}{8}=\frac{y}{6}$
∴y=2.4
设经过y秒后,△CPQ∽△CAB,此时BP=2y,CQ=y.
∴CP=BC-BP=8-2y.
∵△CPQ∽△CAB,
∴$\frac{CP}{CA}=\frac{CQ}{CB}$
∴$\frac{8-2y}{6}=\frac{y}{8}$
∴y=$\frac{32}{11}$
所以,经过2.4秒或者经过$\frac{32}{11}$后两个三角形都相似
点评 本题考查相似三角形的判定,解题的关键是分两种情况进行讨论,本题属于中等题型.

练习册系列答案
相关题目
11.已知双曲线y=$\frac{k}{x}$(k≠0)上有一点P(m,n),m,n是关于t的一元二次方程t2-3t+k=0的两根,且P点到原点的距离为$\sqrt{13}$,则双曲线的表达式为( )
| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
 如图,已知∠B=∠E,AB=DE,要推得△ABC≌△EDF,若以“AAS”为依据,缺条件∠ACB=∠DFE.
如图,已知∠B=∠E,AB=DE,要推得△ABC≌△EDF,若以“AAS”为依据,缺条件∠ACB=∠DFE.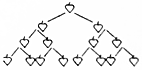 如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果…,猜猜第十行有29个苹果,第2017行有22016个苹果.
如图是一副“苹果图”,第一行有1个苹果,第二行有2个苹果,第三行有4个苹果,第四行有8个苹果…,猜猜第十行有29个苹果,第2017行有22016个苹果.