题目内容
14.解方程:(1)(x+8)(x+1)=0
(2)x2+7x=0
(3)2(x-3)2=8
(4)x2-5x+6=0
(5)3(x-2)2=x(x-2);
(6)(y+2)2=(3y-1)2.
分析 (1)利用因式分解法解方程;
(2)利用因式分解法解方程;
(3)利用直接开平方法解方程;
(4)利用因式分解法解方程;
(5)先移项得到3(x-2)2-x(x-2)=0,然后利用因式分解法解方程;
(6)利用直接开平方法解方程.
解答 解:(1)x+8=0或x+1=0,
所以x1=-8,x2=-1;
(2)x(x+7)=0,
x=0或x+7=0,
所以x1=0,x2=-7;
(3)(x-3)2=4,
x-3=±2,
所以x1=5,x2=1;
(4)(x-2)(x-3)=0,
x-2=0或x-3=0,
所以x1=2,x2=3;
(5)3(x-2)2-x(x-2)=0,
(x-2)(3x-6-x)=0,
x-2=0或3x-6-x=0,
所以x1=2,x2=3;
(6)y+2=±(3y-1),
所以y1=$\frac{3}{2}$,y2=-$\frac{1}{4}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了配方法和公式法解一元二次方程.

练习册系列答案
相关题目
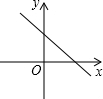
5.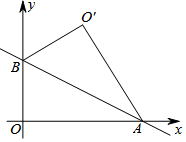 如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
 如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )| A. | $({\sqrt{3}\;,\;\;3})$ | B. | $({3\;,\;\;\sqrt{3}})$ | C. | $({2\;,\;\;2\sqrt{3}})$ | D. | $({2\sqrt{3}\;,\;\;4})$ |
 如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
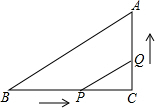 如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?
如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?