题目内容
11.已知双曲线y=$\frac{k}{x}$(k≠0)上有一点P(m,n),m,n是关于t的一元二次方程t2-3t+k=0的两根,且P点到原点的距离为$\sqrt{13}$,则双曲线的表达式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
分析 根据一元二次方程根与系数的关系、勾股定理求出k的值,得到答案.
解答 解:∵m,n是关于t的一元二次方程t2-3t+k=0的两根,
∴m+n=3,mn=k,
∵P点到原点的距离为$\sqrt{13}$,
∴m2+n2=13,即(m+n)2-2mn=13,
∴9-2k=13,
解得,k=-2,
∴双曲线的表达式为y=-$\frac{2}{x}$,
故选:B.
点评 本题考查的是一元二次方程根与系数的故选、反比例函数的解析式的确定,掌握x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$是解题的关键.

练习册系列答案
相关题目
1.下列与:-9+31+28-45相等的是( )
| A. | -9+45+28-31 | B. | 31-45-9+28 | C. | 28-9-31-45 | D. | 45-9-28+31 |
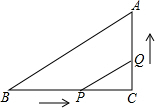 如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?
如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?