题目内容
1. 如图,已知DE⊥AB于E,∠D=∠B,EA=EF,求证:
如图,已知DE⊥AB于E,∠D=∠B,EA=EF,求证:(1)DE=BE;
(2)BC⊥AD.
分析 (1)根据AAS即可证明△AED≌△FEB.
(2)由△AED≌△FEB得∠A=∠BFE=∠DFC,即可证明∠D+∠DFC=90°.
解答 证明: (1)∵DE⊥BA,
(1)∵DE⊥BA,
∴∠BEF=∠AED=90°,
在△AED和△FEB中,
$\left\{\begin{array}{l}{∠D=∠B}\\{∠AED=∠BEF}\\{AE=EF}\end{array}\right.$,
∴△AED≌△FEB,
∴DE=EB.
(2)∵△AED≌△FEB,
∴∠A=∠BFE,
∵∠BFE=∠DFC,
∴∠A=∠DFC,
∵∠A+∠D=90°,
∴∠DFC+∠D=90°,
∴∠DCF=90°,
∴BC⊥AD.
点评 本题考查全等三角形的判定和性质,熟练掌握三角形全等的判定以及性质是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
10.cos60°•sin60°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
8. 已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
 已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )| A. | (2,0) | B. | (3,0) | C. | (4,0) | D. | (5,0) |
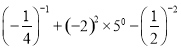
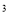 (y-x)
(y-x) 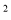 (x-y)+2(x-y)
(x-y)+2(x-y) 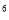
 如图,已知AC、BD相交于O,AE=FC,AO=OC,BO=OD.求证:∠1=∠2.
如图,已知AC、BD相交于O,AE=FC,AO=OC,BO=OD.求证:∠1=∠2. 如图,CD⊥AD于点D,AB⊥AD于点A,∠ACB=∠BAC,CD=CE,连结AE.求证:AE⊥BC.
如图,CD⊥AD于点D,AB⊥AD于点A,∠ACB=∠BAC,CD=CE,连结AE.求证:AE⊥BC.
 把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论:
把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论: