题目内容
20. 如图,点E、F分别在正方形ABCD的边BC、CD上,且BE=CF.
如图,点E、F分别在正方形ABCD的边BC、CD上,且BE=CF.求证:(1)AE=BF;(2)AE⊥EF.
分析 根据正方形的性质可得AB=BC,∠ABE=∠BCF,然后利用“边角边”证明△ABE和△BCF全等,根据全等三角形对应边相等可得AE=BF,全等三角形对应角相等可得∠BAE=∠CAF,然后求出∠BAE+∠ABF=∠ABC=90°,判断出AE⊥BF.
解答 证明:(1)在正方形ABCD中,AB=BC,∠ABE=∠BCF,
在△ABE和△BCF中,$\left\{\begin{array}{l}{AB=BC}\\{ABE=∠BCF}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)∵△ABE≌△BCF,
∴∠BAE=∠CAF,
∴∠BAE+∠ABF=∠CAF+∠ABF=∠ABC=90°,
∴AE⊥BF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,确定出AE与BF所在的三角形并证明三角形全等是解题的关键.

练习册系列答案
相关题目
10. 如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A的度数为( )
如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A的度数为( )
 如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A的度数为( )
如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A的度数为( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
 已知在平面直角坐标系中,四边形OABC的四个顶点坐标分别是O(0,0),A(0,3),B(5,4),C(4,0).
已知在平面直角坐标系中,四边形OABC的四个顶点坐标分别是O(0,0),A(0,3),B(5,4),C(4,0).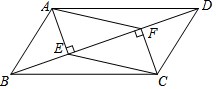 如图,在平行四边形ABCD中,连接对角线BD,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足,求证:四边形AECF是平行四边形.
如图,在平行四边形ABCD中,连接对角线BD,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足,求证:四边形AECF是平行四边形.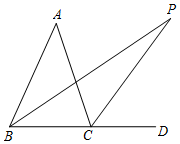 如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
如图①,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.