题目内容
16．古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性，若把第一个三角数记为a1，第二个三角数记为a2…，第10个三角数记为a10，则a9+a10=100．分析 首先计算a1+a2，a2+a3，a3+a4的值，然后总结规律，根据规律可以得出结论．
解答 解：∵a1+a2，=4，
a2+a3=9，
a3+a4，=16，
…
∴an+an+1=（n+1）2=n2+2n+1．
a9+a10=（9+1）2=92+2×9+1=100．
故答案为：100
点评 此题考查数字的变化规律，由特殊计算a1+a2，a2+a3，a3+a4的值可以发现规律：an+an+1=（n+1）2，发现规律是解决本题的关键．
练习册系列答案
相关题目
11．
如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠BAC的正切值是（ ）
如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠BAC的正切值是（ ）| A． | 2 | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{1}{2}$ |
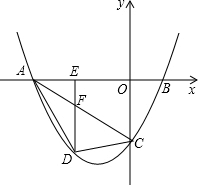已知：如图，直线y=-$\frac{1}{2}$x-3与坐标轴交于点A，C，经过点A，C的抛物线y=ax2+bx-3与x轴交于点B（2，0）．
如图，下面几何体由五个大小相同的小立方块组成，则它的俯视图是（ ）
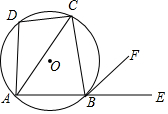如图，四边形ABCD内接于⊙O，点E在AB的延长线上，BF∥AC，AB=BC，∠ADC=130°，则∠FBE=65°．