题目内容
6．如果关于x的不等式组$\left\{\begin{array}{l}{2（a-x）≥-x+4}\\{\frac{3x+4}{2}＜x+1}\end{array}\right.$的解集为x＜-2，那么a的取值范围是a≥1．分析 分别求出每个不等式的解集，根据不等式组的解集为x＜-2可得关于a的不等式，解之可得．
解答 解：解不等式2（a-x）≥-x+4，得：x≤2a-4，
解不等式$\frac{3x+4}{2}$＜x+1，得：x＜-2，
∵不等式组的解集为x＜-2，
则2a-4≥-2，
解得：a≥1，
故答案为：a≥1．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
17．规定运算：对于函数y=xn（n为正整数），规定y′=nxn-1．例如：对于函数y=x4，有y′=4x3．已知函数y=x3，满足y′=18的x的值为（ ）
| A． | x1=3，x2=-3 | B． | x1=x2=0 | C． | x1=$\sqrt{6}$，x2=-$\sqrt{6}$ | D． | x1=3$\sqrt{2}$，x2=-3 |
14．给出一列数0，$\frac{3}{2}$，$\frac{8}{3}$，$\frac{15}{4}$，$\frac{24}{5}$，…，第六个数为（ ）
| A． | $\frac{33}{6}$ | B． | $\frac{35}{6}$ | C． | 12 | D． | $\frac{37}{6}$ |
11．从概率统计的角度解读下列诗词所描述的事件．其中属于确定事件的是（ ）
| A． | 黄梅时节家家雨，青草池塘处处蛙 | B． | 人间四月芳菲尽，山寺桃花始盛开 | ||
| C． | 水面上秤锤浮，直待黄河彻底枯 | D． | 一夜北风紧，开门雪尚飘 |
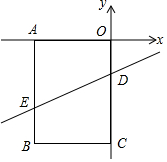如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（-2，-3），直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E，点P在矩形的边AB或BC上，作PF⊥ED于点F，连接PD，当△PFD是等腰三角形时，点P的坐标为（-$\frac{2}{3}$，-3）或（-2，-$\frac{1}{3}$）．
利用数轴解不等式|x-1|＞2．