题目内容
5.(1)如图1,△ABC中,∠A=60°,点E是两条内角平分线的交点,求∠BEC的度数;(2)如图2,∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数.若发生变化,求出变化范围.
(3)图3画两条相交的直线OX、OY,使∠XOY=60°,②在射线OX、OY上分别再任意取A、B两点,③作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数.若发生变化,求出变化范围.
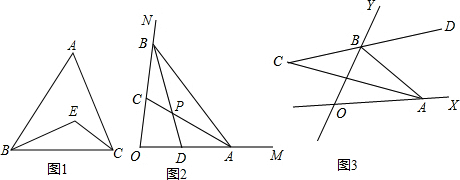
分析 (1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠EBC+∠ECB的度数,由三角形内角和定理即可得出结论;
(2)先根据三角形内角和定理及角平分线的性质求出∠APB的度数,再根据三角形内角和是180°即可求解;
(3)令∠OAC=∠CAB=x,∠ABD=∠BDY=y,再根据三角形的外角性质即可求解.
解答 解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°.
∵点E是两条内角平分线的交点,
∴∠EBC+∠ECB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×120°=60°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-60°=120°;
(2)不变.
∵在△AOB中,∠MON=80°,
∴∠OAB+∠OBA=100°,
又∵AC、BD为角平分线,
∴∠PAB+∠PBA=$\frac{1}{2}$∠OAB+$\frac{1}{2}$∠OBA=$\frac{1}{2}$×100°=50°,
∴∠APB=180°-(∠PAB+∠PBA)=130°,
即随着点A、B位置的变化,∠APB的大小始终不变,为130°;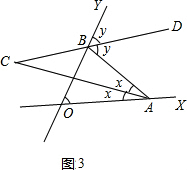
(3)不变.
令∠OAC=∠CAB=x,∠ABD=∠BDY=y,
∵∠ABY是△AOB的外角,
∴2y=n+2x,
同理,∠ABD是△ABC的外角,有y=∠C+x,
∴∠C=$\frac{∠XOY}{2}$=$\frac{60°}{2}$=30°.
点评 本题考查的是三角形的内角和定理及三角形外角的性质,解答此题的关键是熟知以下知识:①三角形的外角等于与之不相邻的两个内角的和;②三角形的内角和是180°.

练习册系列答案
相关题目
13.已知三角形的两边长分别为10和3,第三边的数值是偶数,则该三角形的周长为( )
| A. | 21 | B. | 23 | C. | 21或23 | D. | 21或23或25 |
 如图,数轴上有两点A、B,如果点A表示的数是-3,线段AB=7,那么点B表示的数是4或-10.
如图,数轴上有两点A、B,如果点A表示的数是-3,线段AB=7,那么点B表示的数是4或-10.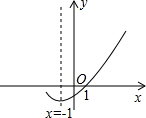 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题: