题目内容
15.已知抛物线y=3x2+3x.则抛物线的对称轴和顶点坐标分别为x=-$\frac{1}{2}$,(-$\frac{1}{2}$,-$\frac{3}{4}$).分析 把函数解析式整理成顶点形式,然后写出对称轴和顶点坐标即可.
解答 解:y=3x2+3x
=3(x2+x+$\frac{1}{4}$)-$\frac{3}{4}$
=3(x+$\frac{1}{2}$)2-$\frac{3}{4}$,
所以抛物线的对称轴为直线x=-$\frac{1}{2}$,顶点坐标为(-$\frac{1}{2}$,-$\frac{3}{4}$).
故答案为x=-$\frac{1}{2}$,(-$\frac{1}{2}$,-$\frac{3}{4}$).
点评 本题考查了二次函数的性质,把函数解析式整理顶点式形式求解更加简便.

练习册系列答案
相关题目
3.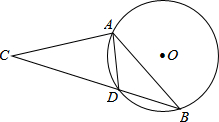 如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
 如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | 2 | D. | $\sqrt{3}$+1 |
10.下列各式的值最小的是( )
| A. | 0-3 | B. | -22 | C. | -4×0 | D. | |-5| |
7.下列各式中计算正确的是( )
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{9}$=±3 | C. | $\root{3}{(-2)^{3}}$=-2 | D. | (2$\sqrt{3}$)2=6 |
 如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).
如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).