题目内容
6.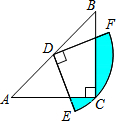 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
分析 连接CD,作DM⊥BC,DN⊥AC,证明△DMG≌△DNH,则S四边形DGCH=S四边形DMCN,求得扇形FDE的面积,则阴影部分的面积即可求得.
解答 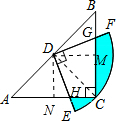 解:连接CD,作DM⊥BC,DN⊥AC.
解:连接CD,作DM⊥BC,DN⊥AC.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴DC=$\frac{1}{2}$AB=1,四边形DMCN是正方形,DM=$\frac{\sqrt{2}}{2}$.
则扇形FDE的面积是:$\frac{90π×{1}^{2}}{360}$=$\frac{π}{4}$.
∵CA=CB,∠ACB=90°,点D为AB的中点,
∴CD平分∠BCA,
又∵DM⊥BC,DN⊥AC,
∴DM=DN,
∵∠GDH=∠MDN=90°,
∴∠GDM=∠HDN,
在△DMG和△DNH中,
$\left\{\begin{array}{l}{∠DMG=∠DNH}\\{∠GDM=∠HDN}\\{DM=DN}\end{array}\right.$,
∴△DMG≌△DNH(AAS),
∴S四边形DGCH=S四边形DMCN=$\frac{1}{2}$.
则阴影部分的面积是:$\frac{π}{4}$-$\frac{1}{2}$.
故答案为$\frac{π}{4}$-$\frac{1}{2}$.
点评 本题考查了三角形的全等的判定与扇形的面积的计算的综合题,正确证明△DMG≌△DNH,得到S四边形DGCH=S四边形DMCN是关键.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{6}$ | B. | x6÷x3=x2 | C. | $\sqrt{4}$=2 | D. | a2(-a2)=a4 |
11.按照如图所示的方法排列黑色小正方形地砖,则第13个图案中黑色小正方形地砖的块数是( )

| A. | 253 | B. | 273 | C. | 293 | D. | 313 |
15.立方根等于它本身的所有数为( )
| A. | -1,0,1 | B. | 0,1 | C. | 0,-1 | D. | 1 |
16.若(x+k)2=x2+2kx+9,则k的值是( )
| A. | 3或-3 | B. | 6或-6 | C. | 9或-9 | D. | 1或-1 |
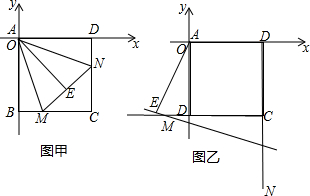
 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.