题目内容
14.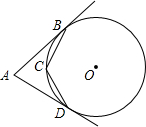 如图,直线AB、AD分别与⊙O切于点B、D,C为⊙O上一点,且∠BCD=132°,则∠A的度数是( )
如图,直线AB、AD分别与⊙O切于点B、D,C为⊙O上一点,且∠BCD=132°,则∠A的度数是( )| A. | 48° | B. | 84° | C. | 90° | D. | 96° |
分析 过点B作直径BE,连接OD、DE.根据圆内接四边形性质可求∠E的度数;根据圆周角定理求∠BOD的度数;根据四边形内角和定理求解即可.
解答 解:过点B作直径BE,连接OD、DE. ∵B、C、D、E共圆,∠BCD=140°,
∵B、C、D、E共圆,∠BCD=140°,
∴∠E=180°-132°=48°,
∴∠BOD=96°,
∵AB、AD与⊙O相切于点B、D,
∴∠OBA=∠ODA=90°,
∴∠A=360°-90°-90°-96°=84°.
故选B.
点评 此题考查了切线的性质、圆内接四边形性质、圆周角定理、四边形内角和定理等知识点,难度中等.连接切点和圆心是解决有关切线问题时常作的辅助线.

练习册系列答案
相关题目
5.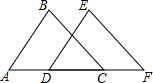 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )| A. | BC=EF | B. | ∠A=∠EDF | C. | AB∥DE | D. | ∠BCA=∠F |
2.如果点(a,1-a)在第四象限,那么a的取值范围是( )
| A. | 0<a<1 | B. | -1<a<0 | C. | a<0 | D. | a>1 |
9.二次函数y=-3(x-4)2+5的开口方向、对称轴、顶点坐标分别是( )
| A. | 向下、直线x=4、(4,5) | B. | 向下、直线x=-4、(-4,5) | ||
| C. | 向上、直线x=4、(4,5) | D. | 向上、直线x=-4、(-4,-5) |
19. 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )
 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )| A. | a-b | B. | a+b | C. | a-2b | D. | 2a-b |




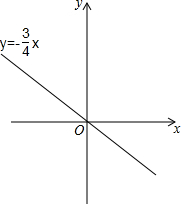 一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C.
一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C. 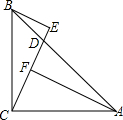 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,BE⊥CD,垂足为点E,AF⊥CD,垂足为点F,若$\frac{BD}{AD}$=$\frac{1}{2}$,AC=6$\sqrt{5}$,则DE=2.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,BE⊥CD,垂足为点E,AF⊥CD,垂足为点F,若$\frac{BD}{AD}$=$\frac{1}{2}$,AC=6$\sqrt{5}$,则DE=2. 如图,是y关于x的函数的图象,则不等式kx+b≤0的解集在数轴上可表示为( )
如图,是y关于x的函数的图象,则不等式kx+b≤0的解集在数轴上可表示为( )


