题目内容
4.正比例函数y=kx(k≠0)和一次函数y=x-k在同一个直角坐标系内的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据正比例函数和一次函数的图象性质并结合其系数作答.
解答 解:当k>0时,正比例y=kx函数图象经过1,3象限,一次函数y=x-k图象经过1,3,4象限,
当k<0时,正比例y=kx函数图象经过2,4象限,一次函数y=x-k图象经过1,3,2象限.
故选D.
点评 本题主要考查了一次函数的图象性质和正比例函数的图象性质,关键是由k的取值确定函数所在的象限.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
14.对于任意不相等的两个实数a、b,定义运算※如下:a※b=$\frac{\sqrt{a+b}}{a-b}$;例如3※2=$\frac{\sqrt{3+2}}{3-2}$=$\sqrt{5}$.那么5※7等于( )
| A. | $-\sqrt{3}$ | B. | -4 | C. | $-2\sqrt{3}$ | D. | -3 |
15.若函数y=$\frac{x-2}{{x}^{2}-1}$的函数值为0,则自变量x的值为( )
| A. | 2 | B. | -1 | C. | ±1 | D. | 1 |
19.在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如下:
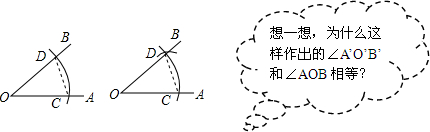
作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )

作法:
(1)如图所示,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧相交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB
对于“想一想”中的问题,下列回答正确的是( )
| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
14.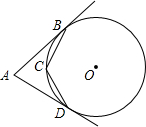 如图,直线AB、AD分别与⊙O切于点B、D,C为⊙O上一点,且∠BCD=132°,则∠A的度数是( )
如图,直线AB、AD分别与⊙O切于点B、D,C为⊙O上一点,且∠BCD=132°,则∠A的度数是( )
 如图,直线AB、AD分别与⊙O切于点B、D,C为⊙O上一点,且∠BCD=132°,则∠A的度数是( )
如图,直线AB、AD分别与⊙O切于点B、D,C为⊙O上一点,且∠BCD=132°,则∠A的度数是( )| A. | 48° | B. | 84° | C. | 90° | D. | 96° |
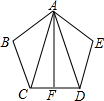 如图,已知AB=AE,BC=ED,∠B=∠E.
如图,已知AB=AE,BC=ED,∠B=∠E. 读语句画图,再填空,如图:
读语句画图,再填空,如图: