题目内容
9．二次函数y=-3（x-4）2+5的开口方向、对称轴、顶点坐标分别是（ ）| A． | 向下、直线x=4、（4，5） | B． | 向下、直线x=-4、（-4，5） | ||
| C． | 向上、直线x=4、（4，5） | D． | 向上、直线x=-4、（-4，-5） |
分析 根据二次函数顶点式解析式分别解答即可．
解答 解：二次函数y=-3（x-4）2+5的开口方向向下；
对称轴是直线x=4；
顶点坐标是（4，5）．
故选：A．
点评 本题考查了二次函数的性质，熟练掌握利用二次函数顶点式形式求解对称轴和顶点坐标的方法是解题的关键．
练习册系列答案
相关题目
19．在学习“用直尺和圆规作一个角等于已知角”时，教科书介绍如下：
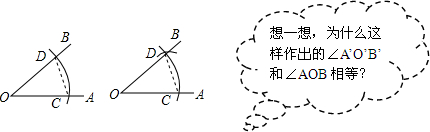
作法：
（1）如图所示，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
（3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；
（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB
对于“想一想”中的问题，下列回答正确的是（ ）
作法：
（1）如图所示，以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；
（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；
（3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；
（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB
对于“想一想”中的问题，下列回答正确的是（ ）
| A． | 根据“边边边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB | |
| B． | 根据“边角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB | |
| C． | 根据“角边角”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB | |
| D． | 根据“角角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB |
20．
如图，在△ABC中，AB=AC，点D在AC边的右侧，连接DA、DB、DC，若AD=DC，∠ADB=∠ACB，AD=5，BD=11，则BC边的长为$\frac{24}{5}$$\sqrt{5}$．
如图，在△ABC中，AB=AC，点D在AC边的右侧，连接DA、DB、DC，若AD=DC，∠ADB=∠ACB，AD=5，BD=11，则BC边的长为$\frac{24}{5}$$\sqrt{5}$．
4．下列变形是属于移项的是（ ）
| A． | 由2x=2，得x=1 | B． | 由$\frac{x}{2}$=-1，得x=-2 | ||
| C． | 由3x-$\frac{7}{2}$=0，得3x=$\frac{7}{2}$ | D． | 由-2x-2=0，得x=-1 |
14．
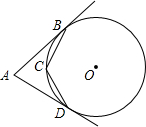如图，直线AB、AD分别与⊙O切于点B、D，C为⊙O上一点，且∠BCD=132°，则∠A的度数是（ ）
如图，直线AB、AD分别与⊙O切于点B、D，C为⊙O上一点，且∠BCD=132°，则∠A的度数是（ ）| A． | 48° | B． | 84° | C． | 90° | D． | 96° |
如图，在△ABC中，∠A=90°，AB=AC，O是BC的中点，如果在AB和AC上分别有一个动点M、N在移动，且在移动时保持AN=BM．
18．下列事件中，是随机事件的是（ ）
| A． | 通常加热到100℃时，水沸腾 | |
| B． | 度量三角形的外角和，结果是360° | |
| C． | 明天太阳从西边升起 | |
| D． | 篮球队员在罚球线上投篮一次，未投中 |
19．下列运算中，结果正确的是（ ）
| A． | 2a2+a=3a2 | B． | 2a-1=$\frac{1}{2a}$ | C． | （-a）3•a2=-a6 | D． | $\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$ |