题目内容
4．
如图，是y关于x的函数的图象，则不等式kx+b≤0的解集在数轴上可表示为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 从图象上得到函数的增减性及与x轴的交点的横坐标，即能求得不等式kx+b≤0的解集．
解答 解：函数y=kx+b（k≠0）的图象，与x轴的交点是（2，0），且函数值y随自变量x的增大而增大，
故不等式kx+b≤0的解集是x≤2．
故选B．
点评 本题考查了一次函数与不等式（组）的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．
练习册系列答案
相关题目
14．
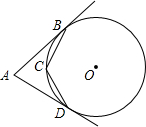如图，直线AB、AD分别与⊙O切于点B、D，C为⊙O上一点，且∠BCD=132°，则∠A的度数是（ ）
如图，直线AB、AD分别与⊙O切于点B、D，C为⊙O上一点，且∠BCD=132°，则∠A的度数是（ ）| A． | 48° | B． | 84° | C． | 90° | D． | 96° |
15．
如图，在?ABCD中，E是AD上一点，且EM∥AD，EN∥CD，则下列式子中错误的是（ ）
如图，在?ABCD中，E是AD上一点，且EM∥AD，EN∥CD，则下列式子中错误的是（ ）| A． | $\frac{AM}{BM}=\frac{DE}{BE}$ | B． | $\frac{AM}{AB}=\frac{CN}{CB}$ | C． | $\frac{ME}{BC}=\frac{NE}{AB}$ | D． | $\frac{BE}{BD}=\frac{NE}{CB}$ |
12．下列各式计算正确的是（ ）
| A． | 3x2-x2=3 | B． | 3a2+2a3=5a5 | C． | 3+x=3x | D． | 0.25ab-$\frac{1}{4}$ba=0 |
19．下列运算中，结果正确的是（ ）
| A． | 2a2+a=3a2 | B． | 2a-1=$\frac{1}{2a}$ | C． | （-a）3•a2=-a6 | D． | $\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$ |
9．零上23℃，记作+23℃，零下8℃，可记作（ ）
| A． | 8 | B． | -8 | C． | 8℃ | D． | -8℃ |
16．（$\sqrt{16}$）2的算术平方根是（ ）
| A． | 4 | B． | ±4 | C． | -4 | D． | 16 |
13．下列各式从左到右的变形一定正确的是（ ）
| A． | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B． | $\frac{a}{2b}=\frac{ac}{2bc}$ | ||
| C． | $-\frac{x+1}{x-y}=\frac{x-1}{x-y}$ | D． | $\frac{{x-\frac{1}{2}y}}{{\frac{1}{2}x+y}}=\frac{2x-y}{x+2y}$ |
如图，在Rt△ABC中，∠BAC=90°，如果将该三角形绕点A按顺时针旋转到△AB1C1的位置，点B1恰好落在边BC的中点处，那么旋转的角度等于60°．