题目内容
2.若关于x的不等式x-$\frac{a}{2}$<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
分析 先解不等式,再利用不等式的解集得到1+$\frac{a}{2}$=1,则a=0,然后计算判别式的值,最后根据判别式的意义判断方程根的情况.
解答 解:解不等式x-$\frac{a}{2}$<1得x<1+$\frac{a}{2}$,
而不等式x-$\frac{a}{2}$<1的解集为x<1,
所以1+$\frac{a}{2}$=1,解得a=0,
又因为△=a2-4=-4,
所以关于x的一元二次方程x2+ax+1=0没有实数根.
故选C.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
17.计算($\frac{1}{2}}$)-1所得结果是( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
14.下列说法正确的是( )
| A. | “经过有交通信号的路口,遇到红灯,”是必然事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次 | |
| C. | 处于中间位置的数一定是中位数 | |
| D. | 方差越大数据的波动越大,方差越小数据的波动越小 |

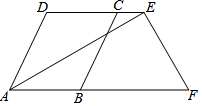 已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,∠DEA=30°,AE⊥EF,垂足为E.
已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,∠DEA=30°,AE⊥EF,垂足为E.