题目内容
12.如图,在△ABC中,∠C=90°,AC=3,BC=4,点D,E分别在AC,BC上(点D与点A,C不重合),且∠DEC=∠A,将△DCE绕点D逆时针旋转90°得到△DC′E′.当△DC′E′的斜边、直角边与AB分别相交于点P,Q(点P与点Q不重合)时,设CD=x,PQ=y.(1)求证:∠ADP=∠DEC;
(2)求y关于x的函数解析式,并直接写出自变量x的取值范围.

分析 (1)根据等角的余角相等即可证明;
(2)分两种情形①如图1中,当C′E′与AB相交于Q时,即$\frac{6}{5}$<x≤$\frac{12}{7}$时,过P作MN∥DC′,设∠B=α.②当DC′交AB于Q时,即$\frac{12}{7}$<x<3时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,分别求解即可;
解答 (1)证明:如图1中,
∵∠EDE′=∠C=90°,
∴∠ADP+∠CDE=90°,∠CDE+∠DEC=90°,
∴∠ADP=∠DEC.
(2)解:如图1中,当C′E′与AB相交于Q时,即$\frac{6}{5}$<x≤$\frac{12}{7}$时,过P作MN∥DC′,设∠B=α
∴MN⊥AC,四边形DC′MN是矩形,
∴PM=PQ•cosα=$\frac{4}{5}$y,PN=$\frac{4}{3}$×$\frac{1}{2}$(3-x),
∴$\frac{2}{3}$(3-x)+$\frac{4}{5}$y=x,
∴y=$\frac{25}{12}$x-$\frac{5}{2}$,
当DC′交AB于Q时,即$\frac{12}{7}$<x<3时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,
∴PN=DM,
∵DM=$\frac{1}{2}$(3-x),PN=PQ•sinα=$\frac{3}{5}$y,
∴$\frac{1}{2}$(3-x)=$\frac{3}{5}$y,
∴y=-$\frac{5}{6}$x+$\frac{5}{2}$.
综上所述,y=$\left\{\begin{array}{l}{-\frac{5}{6}x+\frac{5}{2}}&{(\frac{12}{7}<x<3)}\\{\frac{25}{12}x-\frac{5}{2}}&{(\frac{6}{5}<x≤\frac{12}{7})}\end{array}\right.$
点评 本题考查旋转变换、直角三角形的性质、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.

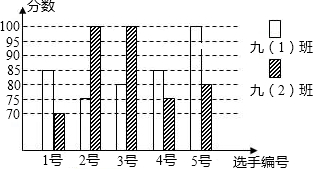 《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.| 平均数 | 中位数 | 众数 | |
| 九(1)班 | 85 | 85 | |
| 九(2)班 | 80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
 下列哪一个是正立方体的展开图( )
下列哪一个是正立方体的展开图( )| A. |  | B. |  | C. |  | D. |  |
| A. | a3+a4=a7 | B. | a4÷a3=a | C. | a3•a2=2a3 | D. | (a3)3=a6 |
 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
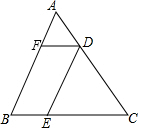 如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.
如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.