题目内容
13.某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个.(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
分析 (1)设九年级师生表演的歌唱类节目有x个,舞蹈类节目有y个,根据“两类节目的总数为20个、唱歌类节目数比舞蹈类节目数的2倍少4个”列方程组求解可得;
(2)设参与的小品类节目有a个,根据“三类节目的总时间+交接用时<150”列不等式求解可得.
解答 解:(1)设九年级师生表演的歌唱类节目有x个,舞蹈类节目有y个,
根据题意,得:$\left\{\begin{array}{l}{x+y=10×2}\\{x=2y-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=12}\\{y=8}\end{array}\right.$,
答:九年级师生表演的歌唱类节目有12个,舞蹈类节目有8个;
(2)设参与的小品类节目有a个,
根据题意,得:12×5+8×6+8a+15<150,
解得:a<$\frac{27}{8}$,
由于a为整数,
∴a的最大值为3,
答:参与的小品类节目最多能有3个.
点评 本题主要考查二元一次方程组和一元一次不等式的应用,理解题意找到题目蕴含的相等关系和不等关系,列出方程组、不等式是解题的关键.

练习册系列答案
相关题目
3.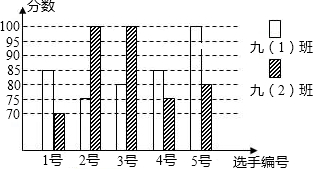 《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写表格;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
 《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.| 平均数 | 中位数 | 众数 | |
| 九(1)班 | 85 | 85 | |
| 九(2)班 | 80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
1. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列计算正确的是( )
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{6}$ | B. | ($\sqrt{2}+1$)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |
2.若关于x的不等式x-$\frac{a}{2}$<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
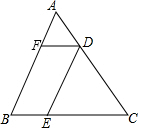 如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.
如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.