题目内容
2.假设图中由四个相邻点围成的正方形面积是一个单位面积,如何计算图①点阵中多边形的面积?你可以把多边形分割成若干小正方形和三角形,分别计算面积后相加,这是一个不错的办法,或者你可以想到通过剪拼的方法来计算,这个想法也很好.
奥地利数学家皮克(Georg Pick,1859-1943)发现了一个计算点阵中多边形面积的公式:S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积.如图①,a=3,b=10,所以多边形面积S=3+$\frac{1}{2}$×10-1=7(单位面积),这个结果与你算出的结果相同吗?
请你在图②的点阵中画一个多边形,并利用皮克公式计算它的面积.
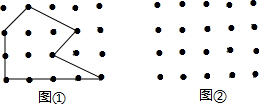
分析 根据图形分割成三角形和四边形,求出各个部分的面积相加即可;先画出多边形,再根据公式求出即可.
解答 解:
图中多边形的面积为:$\frac{1}{2}$×1×1+$\frac{1}{2}×2×1$+2×2+$\frac{1}{2}×1×1$+$\frac{1}{2}$×2×1=7(或3×1+4×1=7),
即根据公式结果与我算出的结果相同;
如图②,多边形的面积S=5+$\frac{1}{2}$×9-1=8.5.
点评 本题考查了作图-应用与设计作图,图形的简拼等知识点,能灵活运用适当的方法求面积是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若关于x的不等式x-$\frac{a}{2}$<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
11. 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
 如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )
如图,∠1与∠2是同旁内角,若∠1=53°,则∠2的大小是( )| A. | 127° | B. | 53° | C. | 127°或53° | D. | 不能确定 |
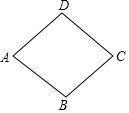 如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.
如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为2$\sqrt{3}$.