题目内容
20.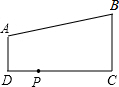 如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有2个.
如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有2个.
分析 如图所示,取DC上一点P,连接AP,BP,设DP=x,CP=8-x,由三角形相似,得到对应边成比例,列出关于x的方程,求出方程的解得到x的值,即可确定出满足题意P的个数.
解答  解:∵AD∥BC,∠D=90°,
解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,
设DP=x,则有CP=8-x,
当△DAP∽△CPB时,有$\frac{AD}{PC}$=$\frac{DP}{BC}$,即$\frac{2}{8-x}$=$\frac{x}{6}$,
解得:x=2或x=6,
此时DP=2或6,
则这样的点P有2个.
故答案为:2.
点评 此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.

练习册系列答案
相关题目
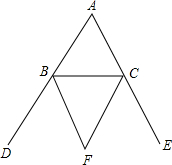 如图,分别作外角∠CBD和∠BCE的平分线BF和CF,交与点F,那么∠A与∠F之间的关系是∠F=90°-$\frac{1}{2}$∠A.
如图,分别作外角∠CBD和∠BCE的平分线BF和CF,交与点F,那么∠A与∠F之间的关系是∠F=90°-$\frac{1}{2}$∠A. 如图,若AB∥CD∥EF,BC∥AD,AC为∠BAD的平分线,则与∠AOF相等的角有( )个.
如图,若AB∥CD∥EF,BC∥AD,AC为∠BAD的平分线,则与∠AOF相等的角有( )个.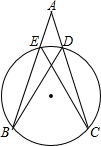 如图,∠A=40°,且$\widehat{BE}$=$\widehat{BC}$=$\widehat{CD}$,则∠ACE的度数为15°.
如图,∠A=40°,且$\widehat{BE}$=$\widehat{BC}$=$\widehat{CD}$,则∠ACE的度数为15°.