题目内容
8.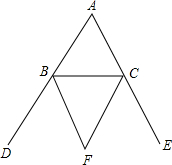 如图,分别作外角∠CBD和∠BCE的平分线BF和CF,交与点F,那么∠A与∠F之间的关系是∠F=90°-$\frac{1}{2}$∠A.
如图,分别作外角∠CBD和∠BCE的平分线BF和CF,交与点F,那么∠A与∠F之间的关系是∠F=90°-$\frac{1}{2}$∠A.
分析 先由角平分线定义得到∠1=∠2,∠3=∠4,再根据三角形内角和定理和三角形外角性质得∠1+∠2=∠A+∠ACB,∠ACB=180°-(∠3+∠4),则2∠1=∠A+180°-2∠3,变形得到2(∠1+∠3)=180°+∠A,接着在△BCF中,利用三角形内角和定理有∠1+∠3=180°-∠F,所以2(180°-∠F)=180°+∠A,然后变形即可得到∠F=90°-$\frac{1}{2}$∠A.
解答 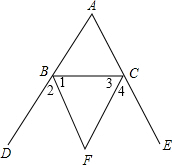 解:∵外角∠CBD和∠BCE的平分线BF和CF,交与点F,
解:∵外角∠CBD和∠BCE的平分线BF和CF,交与点F,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2=∠A+∠ACB,
而∠ACB=180°-(∠3+∠4),
∴2∠1=∠A+180°-2∠3,
∴2(∠1+∠3)=180°+∠A,
∵∠1+∠3+∠F=180°,
∴∠1+∠3=180°-∠F,
∴2(180°-∠F)=180°+∠A,
∴∠F=90°-$\frac{1}{2}$∠A.
故答案为∠F=90°-$\frac{1}{2}$∠A.
点评 本题考查了三角形内角和定理:三角形内角和是180°.解答的关键是沟通外角和内角的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
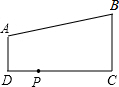 如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有2个.
如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有2个. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面五个结论:①AS=AR;②PQ∥AR;③∠SPC+∠BPR=∠PQC;④S四边形ARPQ=$\frac{1}{2}$S△ABC;⑤BR+CS=SQ.其中正确的结论有( )
如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面五个结论:①AS=AR;②PQ∥AR;③∠SPC+∠BPR=∠PQC;④S四边形ARPQ=$\frac{1}{2}$S△ABC;⑤BR+CS=SQ.其中正确的结论有( )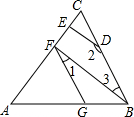 如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,∠FGB=130°,求∠ABC的大小.
如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,∠FGB=130°,求∠ABC的大小.