题目内容
7.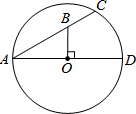 如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )| A. | 2 | B. | 3 | C. | 3.6 | D. | 4 |
分析 首先连接CD,由圆周角定理可得∠C=90°,又由∠CAD=30°,OB⊥AD,OB=4,即可求得OA,AB的长,然后在Rt△ACD中,由三角函数的性质,即可求得答案.
解答 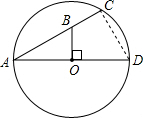 解:连接CD,
解:连接CD,
∵AD是⊙O的直径,
∴∠C=90°,
∵OB⊥AD,
∴∠AOB=∠C=90°,
在Rt△AOB中,∠CAD=30°,OB=4,
∴AB=2OB=8,OA=$\frac{OB}{tan30°}$=4$\sqrt{3}$,
∴AD=2OA=8$\sqrt{3}$,
在Rt△ABC中,AC=AD•cos30°=8$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=12,
∴BC=AC-AB=12-8=4.
故选D.
点评 此题考查了圆周角定理、含30°直角三角形的性质以及三角函数的定义.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在函数y=$\frac{{-{k^2}-1}}{x}$(k为常数)的图象上有三个点(x1,-2),(x2,-1),(x3,3),则x1,x2,x3的大小关系为( )
| A. | x1<x2<x3 | B. | x3<x1<x2 | C. | x3<x2<x1 | D. | x2<x1<x3 |
2.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,5点朝上是必然事件 | |
| B. | 明天下雪的概率为$\frac{1}{2}$,表示明天有半天都在下雪 | |
| C. | 甲、乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 了解一批充电宝的使用寿命,适合用普查的方式 |
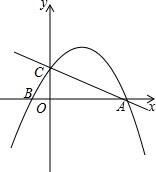 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.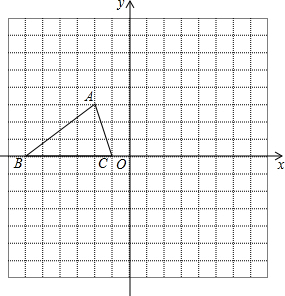 △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上:
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上: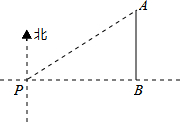 如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.
如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.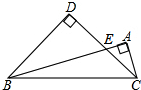 Rt△ABC中,∠ABC=15°,∠BAC=90°,以BC为斜边向A同侧作等腰直角△BDC交AB于E,若BC=$\sqrt{6}$,求S△BEC.
Rt△ABC中,∠ABC=15°,∠BAC=90°,以BC为斜边向A同侧作等腰直角△BDC交AB于E,若BC=$\sqrt{6}$,求S△BEC.